
2008-2009学年度北京101中学第二学期初二期末考试
数学试卷
卷 Ⅰ
一、选择题:在每小题给出的四个选项中,只有一项符合题意,请把你认为正确的选项填入表格内。本大题共10小题,共40分.
1.函数y = 中,自变量
中,自变量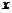 的取值范围是
的取值范围是
A.x≠2 B.x≥
2.某校初二学生为备战体育测试,分小组进行训练. 其中一个小组7名同学的一次训练的成绩(单位:分)为:18,27,30,27,24,28,25. 则这组数据的众数和中位数分别是
A.27,30
B.27,
3.今年6月,我市普降大雨,基本解除了农田旱情.以下是部分区县的降水量分布情况(单位:mm),这组数据的极差是
区县
城区
昌平
怀柔
大兴
丰台
密云
平谷
降水量
28
29.4
31.9
27
28.8
34.1
29.4
A.2.5 B.
4.用配方法解方程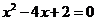 ,下列配方正确的是
,下列配方正确的是
A.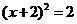 B.
B.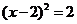 C.
C.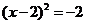 D.
D.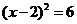
5.将点A(4,0)绕着原点O顺时针方向旋转90°得到对应点A′,则点A′的坐标是
A.(-4,0) B.(4,0) C.(0,-4) D.(0,4)
6.下列图形中,是中心对称图形但不是轴对称图形的是
A.等腰三角形 B.矩形 C.平行四边形 D.等腰梯形
7.某地为发展教育事业,加强了对教育经费的投入,2008年投入3 000万元,预计2010年投入5 000万元.设教育经费的年平均增长率为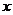 ,根据题意,下面所列方程正确的是
,根据题意,下面所列方程正确的是
A.3000(1+x)2 =5000 B.3000 x2 =5000
C.5000(1+x)2 =3000 D.3000(1+x)+ 3000(1+x)2 =5000
8.已知关于x的一元二次方程 x2 -2x+m = 0有两个不相等的实根,则实数m的取值范围是
A.m>1 B.m<
9.如图,把长为

A. cm B.
cm B.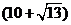 cm C.
cm C.
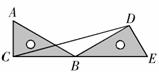
10.如图,在Rt△ABC 中,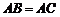 ,D、E是斜边BC上两点,且∠DAE=45°,将△
,D、E是斜边BC上两点,且∠DAE=45°,将△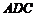 绕点
绕点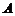 顺时针旋转90
顺时针旋转90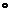 后,得到△
后,得到△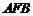 ,连接
,连接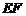 ,下列结论正确的是
,下列结论正确的是
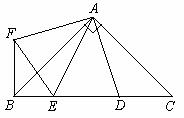
① △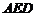 ≌△
≌△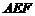 ; ②∠FAB= 45°;
; ②∠FAB= 45°;
③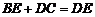 ; ④
; ④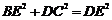 .
.
A.②④ B.①③ C.②③ D.①④
二、填空题:本大题共6小题,每空4分,共32分.
11.设一元二次方程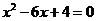 的两个实数根分别为
的两个实数根分别为 和
和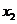 ,则
,则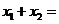 ,
,
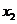 = .
= .
12.方程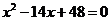 的两个实数根分别是一个三角形的两边长,三角形的另一边长是8,则这个三角形是 三角形.
的两个实数根分别是一个三角形的两边长,三角形的另一边长是8,则这个三角形是 三角形.
13.若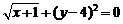 ,则
,则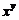 的值等于 .
的值等于 .
14.甲、乙、丙三名射击运动员在某场测试中各射击20次,三人的测试平均环数都是8.5,成绩的方差如下: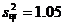 ,
,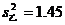 ,
,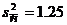 则甲、乙、丙三名运动员测试成绩最稳定的是 .
则甲、乙、丙三名运动员测试成绩最稳定的是 .
15.如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A落在CB的延长线上的点E处,则最小旋转角的度数为 度.
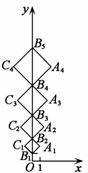
16.如图,在平面直角坐标系xOy中,B1(0,1),B2(0,3),B3(0,6),B4(0,10),…,以B1B2为对角线作第一个正方形A1B
卷 Ⅱ
三、解答题:本大题共8小题,共48分.
17.(5分)计算: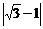 -
- 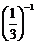 +
+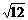 + (-9)0 .
+ (-9)0 .
18.(5分)解方程:x2 ?x -1=0 .
19.(5分)已知x=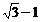 ,求代数式
,求代数式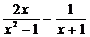 的值.
的值.
20.(6分)在我国,除夕之夜,全家一起看春节联欢晚会是人们传统的娱乐活动,尤其是小品类节目为我们带来了很多的欢乐.为了统计观众对2009年春晚小品类节目的喜好,中央电视台在网上进行了“2009年春晚我最喜爱的小品”调查问卷,并将统计结果绘制成两幅统计图,请你结合图中所给信息解答下列问题:
(1)求参加调查的观众喜欢小品《暖冬》的人数占总投票人数的百分比;
(2)求参加调查的观众喜欢小品《黄豆黄》的人数,并补全条形图;
(3)若北京市共有1200万人收看了春晚节目,请你估算北京市喜欢小品《不差钱》
的观众约有多少人?
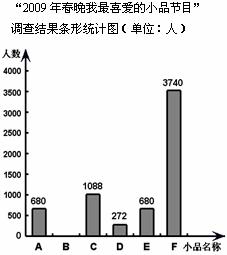
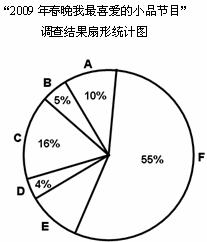
(说明:A:《吉祥三宝》;B:《黄豆黄》;C:《水下除夕夜》; D:《北京欢迎你》;E:《暖冬》;F:《不差钱》)
21.(6分)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:

(1)猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系,请直接写出结论;
(2)将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度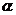 ,得到如图2、图3情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、图3情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并选取图2证明你的判断.
∴ 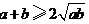 ,只有当
,只有当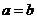 时,等号成立.
时,等号成立.
结论:在 (
( 均为正实数)中,若
均为正实数)中,若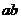 为定值
为定值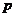 ,则
,则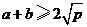 ,
,
只有当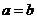 时,
时,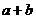 有最小值
有最小值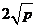 .根据上述内容,回答下列问题:
.根据上述内容,回答下列问题:
(1)若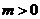 ,只有当
,只有当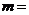 时,
时,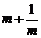 有最小值
.
有最小值
.
(2)探索应用:已知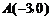 ,
, ,点P为双曲线
,点P为双曲线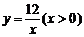 上的任意一点,过点P作
上的任意一点,过点P作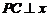 轴于点
轴于点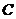 ,
,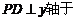 D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
23.(7分)已知关于x的方程 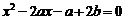 ,其中a、b为实数.
,其中a、b为实数.
(1)若此方程有一个根为
(2)若对于任何实数a ,此方程都有实数根,求b的取值范围.
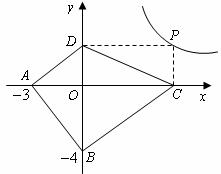
24.(8分)已知:等腰三角形OAB在直角坐标系中的位置如图,点A的坐标为(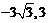 ),点B的坐标为(-6,0).
),点B的坐标为(-6,0).

(1)若三角形OAB关于y轴的轴对称图形是三角形OA′B′,请直接写出A、B的对称点A′、B′的坐标;
(2)若将三角形OAB沿x轴向右平移m个单位,此时点A恰好落在反比例函数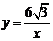 的图象上,求m的值;
的图象上,求m的值;
(3)若三角形OAB绕点O按逆时针方向旋转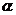 度(0<
度(0<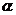 <360).
<360).
①当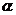 =30°时,点B恰好落在反比例函数
=30°时,点B恰好落在反比例函数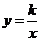 的图象上,求k的值.
的图象上,求k的值.
②问点A、B能否同时落在①中的反比例函数的图象上,若能,求出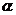 的值;若不能,
的值;若不能,
请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com