
2009年自贡市初中毕业生学业考试
数学试卷
(本试卷满分120分,考试时间120分钟)
第Ⅰ卷(选择题 共30分)
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.我们把零上16°记作+
A.+2 B.-
2.为应对全球金融危机,我国采取宽松信贷货币政策,今年三月份我国信贷激增1.89万亿,将这个数用科学记数法表示出来为 ( )
A.1.89×108 B.1.89×
3.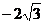 与
与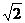 之间最小的整数是 ( )
之间最小的整数是 ( )
A.0 B.-l C.-2 D.-3
4.
A.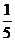 B.
B.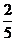 C.
C.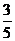 D.
D.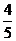
5.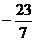 ,3
,3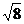 ,
,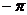 ,sin60°中无理数的个数是 ( )
,sin60°中无理数的个数是 ( )
A.1个 B.2个 C.3个 D.4个
6.数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案,其中正确的是 ( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量三个角是否为直角
7.如图是由几个相同的小正方体搭成几何体的三视图,则搭成这个几何体的小正方体的个数是 ( )
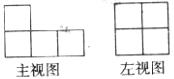
A.4个 B.5个 C.6个 D.7个
8.已知△MNP如图所示,则下列四个三角形中与△MNP相似的是 ( )
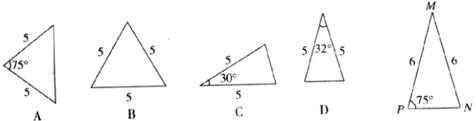
9.如图,若等边△ABC的边长为
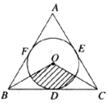
A.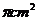 B.
B.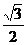
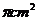 C.
C.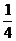
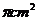 D.
D.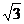
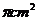
10.如图是陈老师晚饭后出门散步时,离家的距离(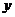 )与时间(
)与时间(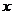 )之间的函数图象.若用黑点表示陈老师家的位置,则陈老师行走的路径可能是 ( )
)之间的函数图象.若用黑点表示陈老师家的位置,则陈老师行走的路径可能是 ( )
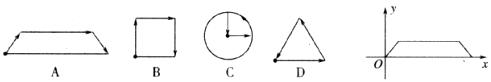
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共5小题,每小题4分,共20分.请把答案填在题中横线上)
11.若第三象限内的点P( ,
,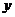 )满足
)满足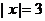 ,y2=5,则点P的坐标是__________.
,y2=5,则点P的坐标是__________.
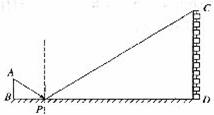
12.如图,小华用手电测量学校食堂的高度,在P处放一水平的平面镜,光线从A出发,经平面镜反射后刚刚射到食堂顶部C处,已知AB⊥BD,CD⊥BD,且AB=1.
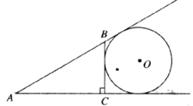
13.如图,⊙O与△ABC中AB、AC的延长线及BC边相切,且∠ACB=90°,∠A,∠B,∠C所对的边长依次为3,4,5,则⊙O的半径是___________
14.为配合全国人口普查,平安村村委会对该村所有的360户家庭人数做了个统计,结果如下:
家庭数(户)
家庭人口数(人)
60
2
180
3
60
4
40
5
20
6
请你根据所学的统计知识提出问题,并填在下面的横线上(不需要解答,也不要解释,但提出的问题应该是利用表中提供数据能求解的,否则视为错误答案).
例:多少人口的家庭最多?
(1)________________________________________________________________________
(2) _______________________________________________________________________
(3) _______________________________________________________________________
(4) _______________________________________________________________________
15.已知一次函数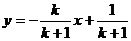 (
( =1,2,3,…,
=1,2,3,…, )的图象与坐标轴所成的直角三角形面积为S1,S2,S3,…,S
)的图象与坐标轴所成的直角三角形面积为S1,S2,S3,…,S ,则S1+S2+S3+…+S2009=_______________.
,则S1+S2+S3+…+S2009=_______________.
三、解答题(本大题共11小题,共70分.解答应写出文字说明、证明过程或演算步骤)
16.(本小题满分5分)
分解因式: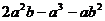
17.(本小题满分5分)
计算: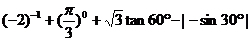
18.(本小题满分5分)
解方程: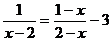
19.(本小题满分5分)
如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置.
(1)旋转中心是哪一点?
(2)旋转的最小角度是多少度?
(3)若M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
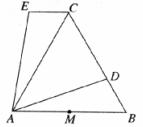
20.(本小题满分6分)
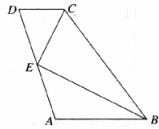
如图,在梯形ABCD中,CD//AB,AB=2,BC=3,CD=1,E是AD的中点,求证:CE⊥BE.
21.(本小题满分6分)
如图,把矩形纸片ABCD沿EF折叠,使点B落在AD边上的点B’处,点A落在A’处.
(1)求证:B’E=BF;
(2)设AE=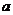 ,AB=b,BF=c,
,AB=b,BF=c,
试猜想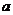 、b、c之间有何等量关系,并给予说明.
、b、c之间有何等量关系,并给予说明.
22.(本小题满分6分)
围棋盒中有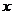 颗白色棋子,
颗白色棋子,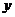 颗黑色棋子,从盒中随机地取出一个棋子,若它是白色棋子的概率是
颗黑色棋子,从盒中随机地取出一个棋子,若它是白色棋子的概率是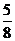 ,
,
(1)试写出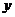 与
与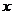 的函数关系;
的函数关系;
(2)第一次取出的棋子放回盒中,再往盒中放入6颗白色棋子,若随机取出一颗白色棋子的概率为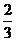 ,求
,求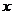 和y的值.
和y的值.
23.(本小题满分7分)
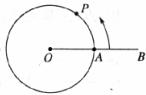
如图,点A是半径为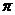 cm/s的速度沿圆周逆时针运动。当P回到点A立即停止运动.
cm/s的速度沿圆周逆时针运动。当P回到点A立即停止运动.
(1)若∠POA=90°,求点P运动的时间;
(2)延长OA至B,使AB=OA,当点P运动的时间为2 s时,判断直线BP与⊙O的位置关系,并说明理由.
24.(本小题满分7分)
我市荣县某水果批发市场,荔枝的价格如下表:
购买荔枝数量(kg)
不超过
每千克价格
6元
5元
4元
张阿姨分两次购买荔枝共
我们知道,在数轴上,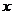 =2表示一个点,而在平面直角坐标系中,
=2表示一个点,而在平面直角坐标系中,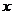 =2表示一条直线;我们还知道,以二元一次方程
=2表示一条直线;我们还知道,以二元一次方程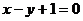 的所有解为坐标的点组成的图形就是一次函数
的所有解为坐标的点组成的图形就是一次函数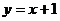 的图象,它也是一条直线,如图1;观察图l可得直线
的图象,它也是一条直线,如图1;观察图l可得直线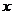 =2与直线
=2与直线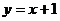 的交点P的坐标(2,3)就是方程
的交点P的坐标(2,3)就是方程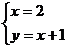 ,的解.
,的解.
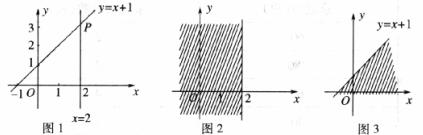
在直角坐标系中,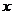 ≤2表示直线
≤2表示直线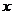 =2以及它左侧的平面区域;
=2以及它左侧的平面区域;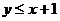 表示直线
表示直线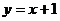 以及它下方的平面区域;分别见图2、3.
以及它下方的平面区域;分别见图2、3.
(1)请在下面所示的坐标系中用作图法求方程组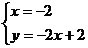 的解.
的解.
(2)用阴影表示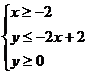 所围成的区域.并求出该区域的面积.
所围成的区域.并求出该区域的面积.
26.(本小题满分9分)
已知抛物线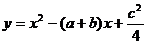 ,其中
,其中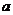 ,b,c分别是△ABC中∠A,∠B,∠C的对边.
,b,c分别是△ABC中∠A,∠B,∠C的对边.
(1)求证:该抛物线与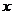 轴必有两个交点;
轴必有两个交点;
(2)设抛物线与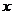 轴的两个交点为P,Q,顶点为R,∠PQR=
轴的两个交点为P,Q,顶点为R,∠PQR=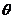 ,已知
,已知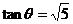 ,△ABC的周长为10,求抛物线的解析式;
,△ABC的周长为10,求抛物线的解析式;
(3)设直线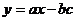 与抛物线交于点E,F,与
与抛物线交于点E,F,与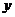 轴交于点M;抛物线与
轴交于点M;抛物线与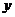 轴交于点N.若抛物线的对称轴为直线
轴交于点N.若抛物线的对称轴为直线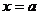 ,△MNE与△MNF的面积之比为5:1,试判断△ABC的形状,并证明你的结论.
,△MNE与△MNF的面积之比为5:1,试判断△ABC的形状,并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com