
填空题的解法
1.内容概要:
填空题只填结果而不要过程,这个结果可以象做解答题那样,由逻辑推理,计算而得到(演绎推理). 但由于不要过程,也可将一般情形特殊化后再求结果(类比推理),还可从
个别事实中归纳出一般性的结论(归纳推理),所以解填空题的基本策略是要在“准”、“巧”、“快”上下功夫巧;解题的要领是:快――运算要快,力戒小题大作;稳――变形要稳,不可操之过急;全――答案要全,力避残缺不齐;活――解题要活,不要生搬硬套;细――审题要细,不能粗心大意.常用的方法有:①直接法,②特例法,③合理猜想法,④图象法.
2.典例精析:
一、直接法
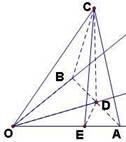 例1:(08四川延考)已知
例1:(08四川延考)已知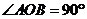 ,
,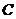 为空间中一点,且
为空间中一点,且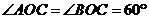 ,则直线
,则直线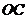 与平面
与平面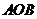 所成角的正弦值为
.
所成角的正弦值为
.
【解析】由对称性点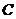 在平面
在平面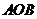 内的射影
内的射影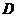 必在
必在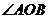 的平分线上作
的平分线上作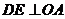 于
于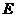 ,连结
,连结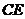 ,则由三垂线定理
,则由三垂线定理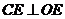 ,
,
设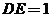 ,则
,则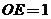 ,
, ,
,
又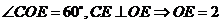 ,
,
所以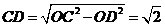 ,因此直线
,因此直线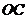 与平面
与平面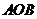 所成角的正弦值
所成角的正弦值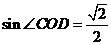 .
.
例2.(08年江苏)若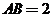 ,
,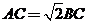 ,则
,则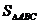 的最大值为 .
的最大值为 .
【解析】由于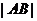 是定值,为求其面积的最大值,只须求出顶点
是定值,为求其面积的最大值,只须求出顶点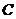 到
到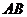 边的距离的最大值即可.而
边的距离的最大值即可.而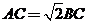 ,说明点
,说明点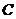 是运动变化的,那么它的轨迹是什么呢?到此我们的思维“进入了”解析几何的领域.
是运动变化的,那么它的轨迹是什么呢?到此我们的思维“进入了”解析几何的领域.
如图1,以点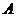 为坐标原点,以
为坐标原点,以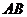 所在直线为
所在直线为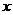 轴,建立平面直角坐标系,则
轴,建立平面直角坐标系,则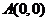 ,
,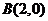 ,由题意不妨设点
,由题意不妨设点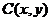 在第一象限(
在第一象限(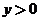 ),则由
),则由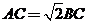 ,得
,得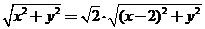 ,即
,即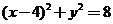 .
.
∴当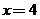 时,
时,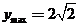 ,此时
,此时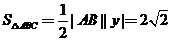 ,
,
所以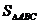 的最大值为
的最大值为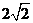 .
.
【点评】本题直接用“形”有一定的难度,若利用“数”运算,建立直角坐标系求解,则问题利于解决.这正好体现出“数形结合”思想,也进一步验证了
一个结论在一般情形下成立,在特殊情形下必成立。填空题只要结果,不要过程,所以当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时,可将填空题中的一般情形特殊化(将图形、图形的位置特殊化或给字母赋于特殊值等)再求解,这种解填空题的方法, 叫特殊化法。凡在一般情形下探求结论的填空题,都可用特例法。
二、特殊化法
例3.(07年海南、宁夏)一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为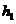 ,
,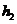 ,
,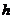 ,则
,则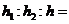 ___________.
___________.
【解析】由于所求的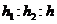 为定值,所以可将三棱柱特殊化为直三棱柱.又三棱锥、四棱锥的底面边长和侧棱都相等,所以取三棱柱为各棱长都相等的正三棱柱.
为定值,所以可将三棱柱特殊化为直三棱柱.又三棱锥、四棱锥的底面边长和侧棱都相等,所以取三棱柱为各棱长都相等的正三棱柱.
设正三棱柱的各棱长为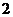 ,则
,则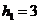 ,
,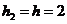 ,
,
∴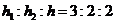 .
.
例4.(07年江西)已知数列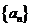 对于任意
对于任意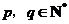 ,有
,有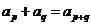 ,若
,若 ,则
,则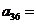 .
.
【解析】由题意,得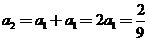 ,
,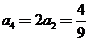 ,
,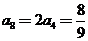 ,
,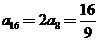 ,
,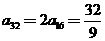 ,∴
,∴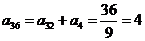 ,从而应当填
,从而应当填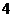 .
.
【点评】我们知道,在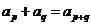 中,取
中,取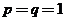 ,得
,得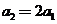 ;取
;取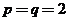 ,得
,得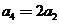 ,等等.这种取特殊值的方法,显示是由一般到特殊的思维方式.事实上,本题的数列
,等等.这种取特殊值的方法,显示是由一般到特殊的思维方式.事实上,本题的数列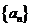 当中,隐含了子数列是等比数列,你能写出一般的通项公式吗?
当中,隐含了子数列是等比数列,你能写出一般的通项公式吗?
例5.(08年全国Ⅰ)在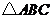 中,
中,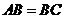 ,
,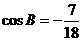 .若以
.若以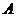 ,
,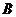 为焦点的椭圆经过点
为焦点的椭圆经过点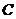 ,则该椭圆的离心率
,则该椭圆的离心率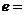 .
.
【解析】设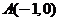 ,
, ,则显然半焦距
,则显然半焦距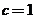 ,
, .
.
∵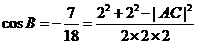 ,∴
,∴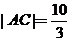 .
.
由椭圆定义,得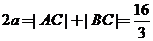 ,∴
,∴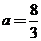 ,
,
故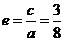 .
.
【点评】本题以三角形为载体考查椭圆的有关知识,一般先设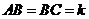 ,由
,由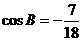 求出
求出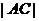 (
(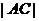 中含有参数
中含有参数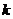 ),然后利用椭圆的概念即可求出离心率
),然后利用椭圆的概念即可求出离心率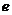 ,这属常规解法.本解答取
,这属常规解法.本解答取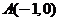 ,
, ,解题思路与常规方法一样,但是由于将
,解题思路与常规方法一样,但是由于将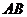
取成常数,计算量降低了,这种解题方法属赋特殊值法,在一定程度上能够简化运算,在复习备考中应该重视这种解题方法.
合理猜想,可以从特殊情形中发现规律,得出一般的正确结论. 合理猜想法多用于探索规律的一类题.
三、合理猜想法
例6.(08年湖北)观察下列等式:
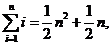
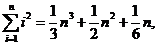
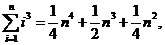
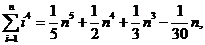
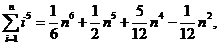
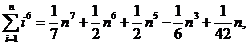
……………………………………
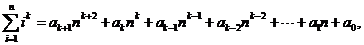
可以推测,当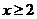 (
(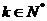 )时,
)时,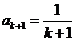 ,
,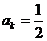 ,
,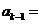 __________,
__________,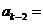 .
.
【解析】观察各个等式右边最高次项的系数为: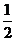 ,
,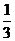 ,
,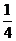 ,
,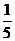 ,……,
,……,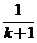 ;各个等式右边次高次项的系数为:
;各个等式右边次高次项的系数为: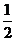 ,
,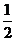 ,
,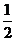 ,
,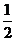 ,……,
,……,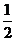 ;第三高次项的系数为:
;第三高次项的系数为: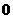 ,
,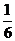 (
( 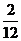 ),
),
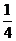 (
(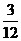 ),
),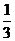 (
( 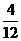 ),……,归纳得出
),……,归纳得出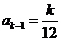 ;各个等式右边第四高次项的系数为:
;各个等式右边第四高次项的系数为: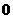 ,
,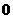 ,
,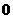 ,
,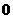 ,……,归纳得出
,……,归纳得出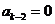 .
.
【点评】此题着重考查学生的观察、归纳、猜测能力以及思维的敏捷性、灵活性.它要求学生善于根据问题的结构特征,从众多的数学信息中提取、挖掘出有效的信息,灵活地运用有关的知识,映衬出相应的意象,找出有效的突破口,从而挖掘规律,发现规律,应用规律.
例7.(08年北京)某校数学课外小组在坐标纸上,为学校的一块空地设计植树方案如下:第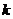 棵树种植在点
棵树种植在点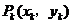 处,其中
处,其中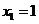 ,
,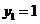 ,当
,当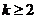 时,
时,
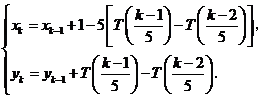
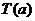 表示非负实数
表示非负实数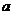 的整数部分,例如
的整数部分,例如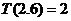 ,
,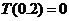 .按此方案,第6棵树种植点的坐标应为________;第2008棵树种植点的坐标应为________.
.按此方案,第6棵树种植点的坐标应为________;第2008棵树种植点的坐标应为________.
【解析】①当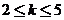 时,
时,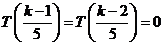 ,则
,则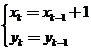 ,解得
,解得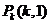 ;
;
②当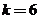 时,
时,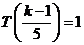 ,
,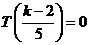 ,则
,则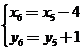 ,解得
,解得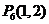 ;
;
③当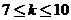 时,
时,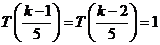 ,则
,则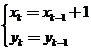 ,解得
,解得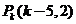 ;
;
④当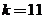 时,
时,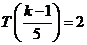 ,
,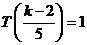 ,则
,则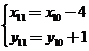 ,解得
,解得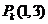 ;
;
…………,如此类推。如通过观察、归纳总结得出一般的规律为:
当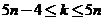 (
(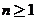 )时,第
)时,第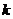 棵树种植在点为
棵树种植在点为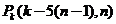 ,于是当
,于是当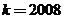 时,
时,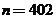 ,从而第2008棵树种植点的坐标应为
,从而第2008棵树种植点的坐标应为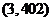 .
.
【点评】此题是将周期数列加以变更、迁移、整合而成,有创意,有新意,给学生探索问题提供了广阔的空间和自由度,特别对学生观察、归纳、猜测、综合分析等能力以及耐心、毅力得到全面的考查,有利于甄别学生的思维层次和数学素养 .本题要求学生善于根据问题的结构特征,从众多的信息中提取、挖掘出有效的信息,从而找出问题的切入点,开启成功之门.
根据试题的特点,找出其几何意义,画出符合题意的辅助图形,借助图形的直观性进行分析探究,得出正确结论.这是一种数形结合的解题策略,在填空题中有着广泛的应用.
四、图象法
例8.设等差数列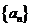 的前
的前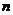 项和为
项和为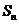 ,若
,若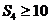 ,
,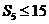 ,则
,则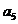 的最大值为________.
的最大值为________.
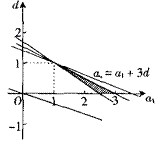
【解析】由已知得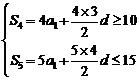 ,∴
,∴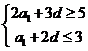 .
.
在坐标系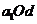 中分别作出直线
中分别作出直线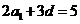 ,
,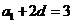 ,得可行域及两直线的交点
,得可行域及两直线的交点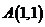 .设目标函数
.设目标函数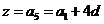 ,作直线
,作直线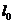 :
: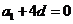 ,当平移直线
,当平移直线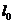 经过点
经过点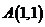 时,
时,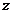 有最大值5,即
有最大值5,即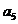 的最大值为5,选B.
的最大值为5,选B.
【点评】若试题给出的是单纯的线性规划问题,则百味全无.而命题者悄悄地将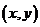 换成
换成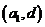 ,同学们在解题过程中必须看透这一伎俩,将数列问题转化为线性规划问题,顿觉简单异常.本题设计遵循基础与能力并重,知识与能力并举的原则,意在考查等差数列的通项公式、前
,同学们在解题过程中必须看透这一伎俩,将数列问题转化为线性规划问题,顿觉简单异常.本题设计遵循基础与能力并重,知识与能力并举的原则,意在考查等差数列的通项公式、前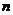 项和公式以及不等式性质等知识,但实在考查数形结合的思想方法.
项和公式以及不等式性质等知识,但实在考查数形结合的思想方法.
【总结提炼】综上,我们主要介绍了填空题几种常见的解法,当然解法会很多,所以我们要在平时注意发现、探索、总结,小题终究是小题,只要多思考,多挖掘新方法、巧方法,那我们解题时才有事半功倍的效果.
3.跟踪练习:
1.设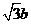 是
是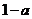 和
和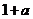 的等比中项,则
的等比中项,则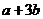 的最大值为__________.
的最大值为__________.
2.函数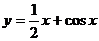 在
在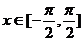 上的最大值为_____________.
上的最大值为_____________.
3.已知函数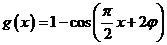 (
(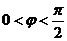 )的图象过点
)的图象过点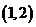 ,若有4个不同的正数
,若有4个不同的正数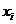 满足
满足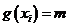 ,且
,且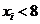 (
(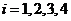 ),则
),则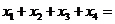 _________.
_________.
4.若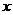 、
、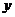 满足条件
满足条件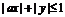 (
(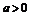 ),则
),则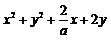 的最大值为__
的最大值为__
5.有20张卡片上分别写有数字1 ,2 ,……,20 ,将它们放入一个盒子内. 有4 个人从中不放回地各抽取一张卡片,抽到两个较小数字的两人在同一组,抽到两个较大数字的两人在同一组. 现其中有两人抽到5、14 ,则此两人在同一组的概率等于__________(用最简分数作答).
6.已知三个正数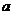 ,
,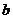 ,
,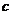 满足条件
满足条件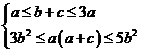 ,则
,则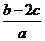 的最小值为______.
的最小值为______.
1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即 的最大值为2.
的最大值为2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴ ;若
;若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
4. 不等式 (
( )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵
 ,
,
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
设 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点 时,
时, 取得最小值.
取得最小值.
解方程组 ,得
,得 ,∴
,∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com