
河北区2008―2009学年度高三年级总复习质量检测二
数 学(文史类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷 (选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的
(1)与 的值相等的是( )
的值相等的是( )
(A)  (B)
(B)  (C)
(C)  (D)
(D) 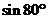
(2)“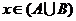 ”是“
”是“ ”的( )
”的( )
(A)必要非充分条件 (B)充分非必要条件
(C)充要条件 (D)既不充分也不必要条件
(3)设 用二分法求方程
用二分法求方程 在
在 内近似解的过程中,经计算得到
内近似解的过程中,经计算得到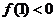 ,
, ,
, ,则可判断方程的根落在区间( )
,则可判断方程的根落在区间( )
(A) 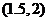 (B)
(B) 
(C)  (D)不能确定
(D)不能确定
(4)函数 的大致图象是( )
的大致图象是( )
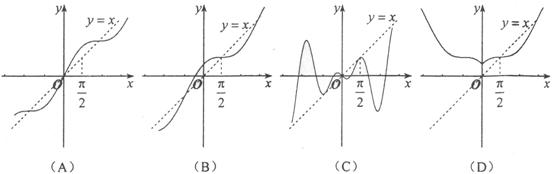 |
(5)在等差数列 中,已知
中,已知 ,则其前9项和
,则其前9项和 的值为( )
的值为( )
(A) 36 (B) 16 (C) 12 (D) 9
(6)在平面直角坐标系中,若不等式组 表示一个平面区域,则这个平面区域面积的值为( )
表示一个平面区域,则这个平面区域面积的值为( )
(A) 8 (B) 12 (C) 16 (D) 32
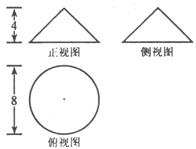 (7)右图是一个物体的三视图,根据
(7)右图是一个物体的三视图,根据
图中尺寸,计算它的体积等于( )
(A)  (B)
(B) 
(C)  (D)
(D) 
(8)已知幂函数 的图象不过原点,则
的图象不过原点,则 的值为( )
的值为( )
(A)6 (B)3 (C)3或6 (D)3或0
(9)若向量 ,
, ,则
,则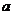 在
在 方向上的投影为( )
方向上的投影为( )
(A) 2 (B) 
(C)  (D) 10
(D) 10
(10)已知直线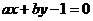 (
( )与圆
)与圆 有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有( )
有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有( )
(A)4条 (B)6条
(C)8条 (D)10条
第Ⅱ卷(非选择题 共100分)
二、填空题:本大题共6小题,每小题4分,共24分。把答案填在题中横线上。
(11)一个容量为 的样本,分成若干组,已知某组频数和频率分别为36和0.25,则
的样本,分成若干组,已知某组频数和频率分别为36和0.25,则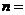 .
.
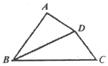 (12)已知直线
(12)已知直线 :
: 和圆
和圆 :
: ,则直线和圆的位置关系为
.
,则直线和圆的位置关系为
.
(13)如图, 平分
平分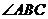 ,
, ,
, ,
,
如果 ,则
,则 的长为
.
的长为
.
(14)已知向量 ,
, ,且
,且 ,则
,则 的值为 .
的值为 .
(15)用直接法求函数 当
当 时的值,需做乘法21次,而改用秦九韶算法后,只需做乘法 次。
时的值,需做乘法21次,而改用秦九韶算法后,只需做乘法 次。
(16)一个计算机程序产生一个5位的随机二进制数
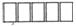 ,其中每位数都是0或1,且出现0或1的概率相等,例如
,其中每位数都是0或1,且出现0或1的概率相等,例如 的最小值为
的最小值为 ,
, 的最大值为
的最大值为 ,则这个随机数
,则这个随机数 小于十进制数12的概率为
.
小于十进制数12的概率为
.
(17)(本小题满分12分)
三、解答题:本大题共6小题,共76分.解答应写出文字说明,证明过程或演算步骤。
已知函数 ,且
,且 。
。
(Ⅰ)求函数 的周期
的周期 和单调递增区间;
和单调递增区间;
(Ⅱ)若 ,且
,且 ,求
,求 的值。
的值。
(18)(本小题满分12分)
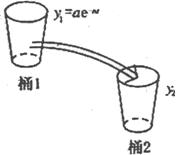
如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有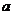 升水,桶2是空的,
升水,桶2是空的, 分钟后桶1中剩余的水符合指数衰减曲线
分钟后桶1中剩余的水符合指数衰减曲线 (其中
(其中 是常数,
是常数, 是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
是自对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
 (Ⅰ)桶2中的水
(Ⅰ)桶2中的水 与时间
与时间 的函数关系式;
的函数关系式;
(Ⅱ)再过多少分钟,桶1中的水是 ?
?
(19)(本小题满分12分)
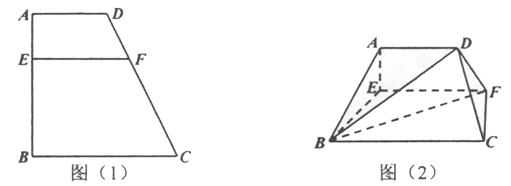
已知如图(1),梯形 中,
中,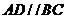 ,
,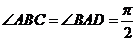 ,
, ,
,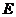 、
、 分别是
分别是 、
、 上的动点,且
上的动点,且 ,设
,设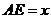 (
(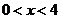 )。沿
)。沿 将梯形
将梯形 翻折,使平面
翻折,使平面 平面
平面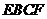 ,如图(2)。
,如图(2)。
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)若以 、
、 、
、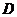 、
、 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为 ,求
,求 的最大值;
的最大值;
(Ⅲ)当 取得最大值时,求异面直线
取得最大值时,求异面直线 和
和 所成角的余弦值.
所成角的余弦值.
 |
(20)(本小题满分12分)
已知函数 (
( ),
), 。
。
(Ⅰ)若 ,且
,且 是
是 的切线,求
的切线,求 的值;
的值;
(Ⅱ)若 ,且
,且 是
是 的切线,求
的切线,求 的值.
的值.
(21)(本小题满分14分)
己知 、
、 、
、 是椭圆
是椭圆 :
: (
(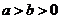 )上的三点,其中点
)上的三点,其中点 的坐标为
的坐标为 ,
, 过椭圆的中心,且
过椭圆的中心,且 ,
, 。
。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 的直线
的直线 (斜率存在时)与椭圆
(斜率存在时)与椭圆 交于两点
交于两点 ,
, ,设
,设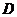 为椭圆
为椭圆 与
与 轴负半轴的交点,且
轴负半轴的交点,且 ,求实数
,求实数 的取值范围.
的取值范围.
(22)(本小题满分14分)
数列 中,
中, ,
, (
( )。
)。
(Ⅰ)求 ,
, ,
, ,
, ;
;
(Ⅱ)求数列 的前
的前 项和
项和 ;
;
(Ⅲ)设 ,存在数列
,存在数列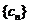 使得
使得 ,试求数列
,试求数列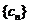 的前
的前 项和
项和 .
.
河北区2008―2009学年度高三年级总复习质量检测二
数 学(文答案)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
A
C
B
D
C
D
B
A
C
一、选择题:本大题共10小题,每小题5分,共50分.
(1)提示:
(2)提示: 由“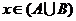 ” 不能推出“
” 不能推出“ ”, 反之则可以.
”, 反之则可以.
(3)提示:∵ ,
, ,∴方程的根落在
,∴方程的根落在 。
。
(4)提示:判断函数 为非奇非偶函数且过点
为非奇非偶函数且过点 ,故选B.
,故选B.
(5)提示:∵ ,∴
,∴
(6)提示:作出可行域,可得面积为16.
(7)提示:由三视图知物体为圆锥,体积为
(8)提示:∵ ∴
∴
(9)提示: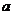 在
在 方向上的投影为
方向上的投影为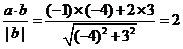
(10)提示:当 ,
, 时,圆上横、纵坐标均为整数的点只有
时,圆上横、纵坐标均为整数的点只有 ,依圆的对称性知圆上共有4个点横纵坐标均为整数,经过其中任意两点的割线有6条,过每一点的切线共有4条,又考虑到直线
,依圆的对称性知圆上共有4个点横纵坐标均为整数,经过其中任意两点的割线有6条,过每一点的切线共有4条,又考虑到直线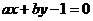 不经过原点,而上述直线中经过原点的有2条,所以满足题意的直线共有
不经过原点,而上述直线中经过原点的有2条,所以满足题意的直线共有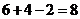 条。
条。
二、填空题:本大题共6小题,每小题4分,共24分.
(11)  ; 提示:
; 提示: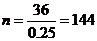 。
。
(12)相交; 提示:依题意可知圆心为 ,
, 与
与 的距离为
的距离为 ,
,
∵圆的半径为3,∴直线和圆的位置关系为相交.
(13)  ;提示: 由已知,得
;提示: 由已知,得 ∽
∽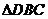 ,∴
,∴
∴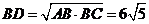
(14)  ;提示:∵
;提示:∵ ,
,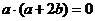 ,∴
,∴
(15)6; 提示: 用秦九韶算法,将原式变形为
 ,只需做6次乘法。
,只需做6次乘法。
(16)  ;提示:由已知条件可知,
;提示:由已知条件可知, 的最小值为0,最大值为31,共有32个数,且产生哪个数的概率是等可能的,所以
的最小值为0,最大值为31,共有32个数,且产生哪个数的概率是等可能的,所以 小于十进制数12的概率为
小于十进制数12的概率为
三、解答题:本大题共6小题,共76分。
(17)解.(Ⅰ)
 .……………………………(理)2分
.……………………………(理)2分
∵ ,∴
,∴ ,解得
,解得 . …………(文)2分
. …………(文)2分
∴ .………………………………4分
.………………………………4分
∴函数 的周期
的周期 ,………………………………………………………6分
,………………………………………………………6分
单调递增区间为 ,
, . ……………………8分
. ……………………8分
(Ⅱ)依题意得
∵ ,∴
,∴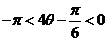 …………………………10分
…………………………10分
∴ 或
或
解得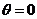 或
或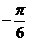 .…………………………………………………………………12分
.…………………………………………………………………12分
(18)
解:(Ⅰ)∵桶2中的水是从桶1中流出的水,而桶1开始的水是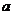 ,又满足
,又满足 ,
,
∴桶2中的水与 的函数关系式是
的函数关系式是 . ………………………………4分
. ………………………………4分
(Ⅱ)∵ 时,
时, ,
,
∴
解得 ,
, 。
。
∴ .…………………………………………………8分
.…………………………………………………8分
当 时,有
时,有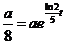 ,解得
,解得 分钟。
分钟。
所以,再过15分钟桶1中的水是 . ………………………………………12分
. ………………………………………12分
(19)
解:(Ⅰ)∵平面 平面
平面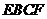 ,
, ,∴
,∴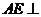 平面
平面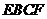 ,
,
∴
∵ ,
,
∴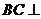 平面
平面 。
。
又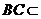 平面
平面 ,
,
∴平面 平面
平面 . ……………………………………………………4分
. ……………………………………………………4分
(Ⅱ)∵ 平面
平面 ,
,
∴ ………………………………………6
………………………………………6

即 时,
时, 有最大值
有最大值 . ………………………………………………8分
. ………………………………………………8分
(Ⅲ)取 中点
中点 ,作
,作 交
交 于
于 ,连结
,连结 ,
, ,
,
∵ ,且
,且 ,
,
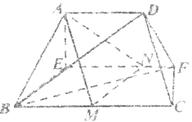 ∴
∴ 为平行四边形. ∴
为平行四边形. ∴
∴ 即为异面直线
即为异面直线 和
和 所成的角.
所成的角.
…………10分
计算得 ,
,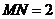 ,
, ,
,
∴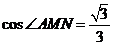 ……………………12分
……………………12分
(20)解:(Ⅰ) ,
,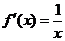 …………………………2分
…………………………2分
令 ,得
,得 ,
,
∴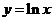 的斜率为1的切线为
的斜率为1的切线为 …………………………………4分
…………………………………4分
∴ .………………………………………………………6分
.………………………………………………………6分
(Ⅱ)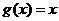 ,
, 。
。
令 ,得
,得 ,
, 。
。
∴ 的斜率为1的切线为
的斜率为1的切线为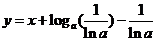 …………………8分
…………………8分
∴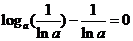 ,即
,即 …………………10分
…………………10分
∴ .…………………………………………………………………………12分
.…………………………………………………………………………12分
(21)解:(Ⅰ)∵ 且
且 过
过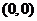 ,则
,则 .…………2分
.…………2分
∵ ,
,
∴ ,即
,即 .…………………………………4分
.…………………………………4分
 又∵
又∵ ,设椭圆
,设椭圆 的方程为
的方程为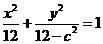 ,
,
将C点坐标代入得 ,
,
解得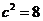 ,
, .
.
∴椭圆 的方程为
的方程为 . …………………………………6分
. …………………………………6分
(Ⅱ)由条件 ,
,
当 时,显然
时,显然 ;……………………………………………………8分
;……………………………………………………8分
当 时,设
时,设 :
: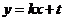 ,
,
 ,消
,消 得
得
由 可得,
可得, ……①………………………………………10分
……①………………………………………10分
设 ,
,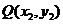 ,
, 中点
中点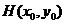 ,
,
则 ,
,
∴ .…………………………………12分
.…………………………………12分
由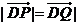 ,
,
∴ ,即
,即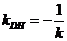 。
。
∴ ,化简得
,化简得 ……②
……②
∴
将①代入②得, 。
。
∴ 的范围是
的范围是 。
。
综上 . ………………………………………………………………14分
. ………………………………………………………………14分
(22)解:(Ⅰ)当 时,有
时,有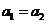 ;当
;当 时,有
时,有 ;……
;……
∴ ,
, ,
, ,
,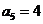 .……………………………………………4分
.……………………………………………4分
(Ⅱ)∵ ,……………………………………………………6分
,……………………………………………………6分
∴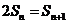 ∴
∴ ……………………………………8分
……………………………………8分
∴ 是首项为
是首项为 ,公比为2的等比数列。
,公比为2的等比数列。
∴ ………………………………………10分
………………………………………10分
(Ⅲ)由 ,得
,得
∴ ,
, ,
,
∵
∴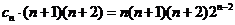 ,
,
即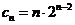 . …………………………………………………12分
. …………………………………………………12分
 …………………①
…………………①
则 …②
…②
②一①得
 .………………………14分www.1010jiajiao.com
.………………………14分www.1010jiajiao.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com