
北京一零一中2008-2009学年度统考二
高三数学(文科)
一、选择题:本大题共8小题,共40分。
1.集合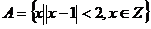 的真子集的个数是
( )
的真子集的个数是
( )
A.3
B
2.等差数列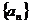 中,已知
中,已知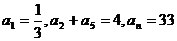 ,则n为
( )
,则n为
( )
A.48
B
3.函数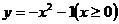 的反函数图象大致为
( )
的反函数图象大致为
( )
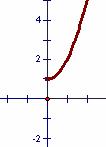
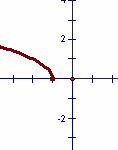
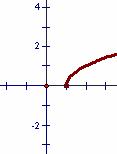
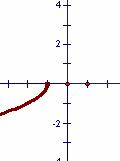
A B C D
4.若函数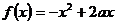 与函数
与函数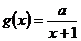 在区间
在区间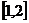 上都是减函数,则实数a的取值范围是
( )
上都是减函数,则实数a的取值范围是
( )
A.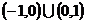 B.
B.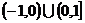 C.
C.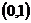 D.
D.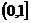
5. 设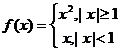 ,
, 是二次函数,若
是二次函数,若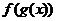 的值域是
的值域是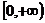 ,则
,则 的值域是( )
的值域是( )
A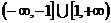 B
B 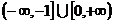 C
C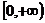 D
D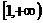
6.若函数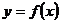 的图像与
的图像与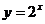 的图像关于y轴对称,若
的图像关于y轴对称,若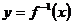 是
是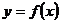 的反函数,则
的反函数,则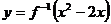 的单调递增区间是
( )
的单调递增区间是
( )
A.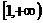 B.
B.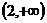 C.
C.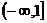 D
D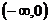
7.已知数列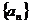 中,
中,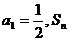 为数列的前n项和,且
为数列的前n项和,且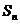 与
与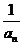 的一个等比中项为n,则
的一个等比中项为n,则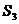 的值为
( )
的值为
( )
A.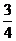 B.
B.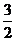 C.
C.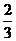 D 1
D 1
8、已知函数①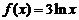 ;②
;②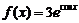 ;③
;③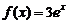 ;④
;④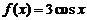 .其中对于
.其中对于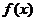 定义域内的任意一个自变量
定义域内的任意一个自变量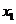 ,都存在唯一一个自变量
,都存在唯一一个自变量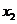 ,使
,使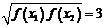 成立的函数是
( )
成立的函数是
( )
A.①② B.①②③ C.③ D.④
二.填空题(本大题共6小题,每小题5分,共30分。把答案填在题中横线上)
9.函数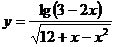 的定义域为______________
的定义域为______________
10.设集合A=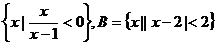 ,那么“
,那么“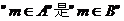 的_____________条件
的_____________条件
11.数列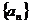 的前n项和
的前n项和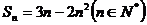 ,则
,则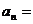 _____________;此时
_____________;此时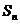 与
与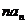 大小关系是_____________
大小关系是_____________
12.设
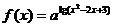 有最大值,则不等式
有最大值,则不等式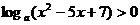 的解集为________________
的解集为________________
13.对于函数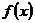 定义域中任意的
定义域中任意的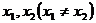 有如下结论:
有如下结论:
①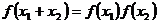 ②
②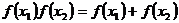 ③
③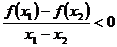
④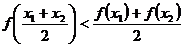 当
当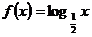 时,上述结论中正确的序号是____________(写出全部正确结论的序号)
时,上述结论中正确的序号是____________(写出全部正确结论的序号)
14.若关于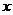 的方程
的方程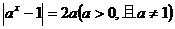 有两个不相等的实数根,则a的取值范围是____________
有两个不相等的实数根,则a的取值范围是____________
三.解答题(本大题共6小题,共80分)
15.(本小题满分13分)已知数列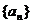 是等差数列,且
是等差数列,且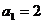 ,
,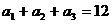
(1)求数列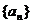 的通项公式;
的通项公式;
(2)设数列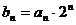 (
(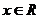 ),求数列
),求数列 的前
的前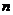 项和公式.
项和公式.
16. (本题满分13分)已知函数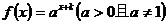 的图像过点
的图像过点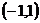 ,其反函数
,其反函数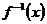 的图像过点
的图像过点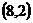 . (1)求
. (1)求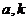 的值
的值
(2)若将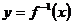 的图像向左平移2个单位,再向上平移1个单位,就得到函数
的图像向左平移2个单位,再向上平移1个单位,就得到函数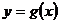 的图像,写出
的图像,写出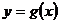 的解析式
的解析式
(3)若函数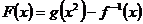 ,求
,求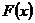 的最小值及取得最小值时x的值
的最小值及取得最小值时x的值
17. (本题满分14分)已知函数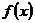 对一切实数
对一切实数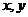 均有
均有 成立,且
成立,且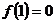 . (1)求
. (1)求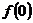 的值 (2)求
的值 (2)求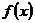 的解析式
的解析式
(3)若函数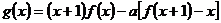 在区间
在区间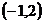 上是减函数,求实数a的取值范围
上是减函数,求实数a的取值范围
18. (本题满分14分)已知二次函数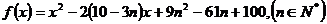
(1)设函数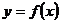 的图像的顶点的横坐标构成数列
的图像的顶点的横坐标构成数列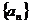 ,求证数列
,求证数列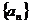 是等差数列
是等差数列
(2)设函数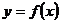 的图像的顶点到y轴距离构成数列
的图像的顶点到y轴距离构成数列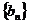 ,求数列
,求数列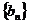 的前n项和
的前n项和
(3)在(1)的条件下,若数列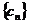 满足
满足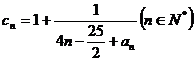 ,求数列
,求数列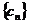 中值最大的项和最小项
中值最大的项和最小项
19. (天津)设函数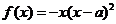 (
(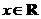 ),其中
),其中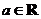 .
.
(1) 当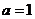 时,求曲线
时,求曲线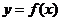 在点
在点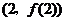 处的切线方程;
处的切线方程;
(2) 当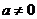 时,求函数
时,求函数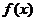 的极大值和极小值;
的极大值和极小值;
(3) 当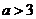 时,证明存在
时,证明存在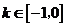 ,使得不等式
,使得不等式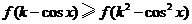 对任意的
对任意的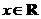 恒成立.
恒成立.
20、对于函数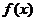 ,若存在
,若存在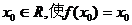 成立,则称
成立,则称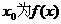 的不动点.如果函数
的不动点.如果函数
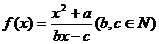 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且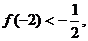
(1)求函数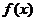 的解析式;
的解析式;
(2)已知各项不为零的数列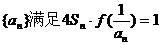 ,求数列通项
,求数列通项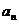 ;
;
(3)如果数列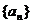 满足
满足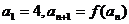 ,求证:当
,求证:当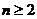 时,恒有
时,恒有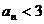 成立.
成立.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com