1.

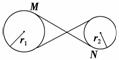
图4－2－16

图示4－2－16所示为某一皮带传动装置．主动轮的半径为r₁，从动轮的半径为r₂.已知主动轮做顺时针转动，转速为n，转动过程中皮带不打滑．下列说法正确的是(　)　　　　　　　　　　　　　　　

A．从动轮做顺时针转动　 　　　　　　　　　　 B．从动轮做逆时针转动

C．从动轮的转速为n　 　　　　　　　　 D．从动轮的转速为n

解析：本题考查的知识点是圆周运动．因为主动轮顺时针转动，从动轮通过皮带的摩擦力带动转动，所以从动轮逆时针转动，选项A错误B正确；由于通过皮带传动，皮带与轮边缘接触处的速度相等，所以由2πnr₁＝2πn₂r₂，得从动轮的转速为n₂＝，选项C正确D错误．

答案：BC

5．

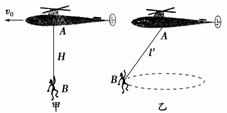
图4－2－15

在一次抗洪救灾工作中，一架直升机A用长H＝50 m的悬索(重力可忽略不计)系住一质量m＝50 kg的被困人员B，直升机A和被困人员B以v₀＝10 m/s的速度一起沿水平方向匀速运动，如图4－2－15甲所示．某时刻开始收悬索将人吊起，在5 s时间内，A、B之间的竖直距离以l＝50－t²(单位：m)的规律变化，取g＝10 m/s².

(1)求这段时间内悬索对被困人员B的拉力大小．

(2)求在5 s末被困人员B的速度大小及位移大小．

(3)直升机在t＝5 s时停止收悬索，但发现仍然未脱离洪水围困区，为将被困人员B尽快运送到安全处，飞机在空中旋转后静止在空中寻找最近的安全目标，致使被困人员B在空中做圆周运动，如图乙所示．此时悬索与竖直方向成37°角，不计空气阻力，求被困人员B做圆周运动的线速度以及悬索对被困人员B的拉力．(sin 37°＝0.6，cos 37°＝0.8)

解析：(1)被困人员在水平方向上做匀速直线运动，在竖直方向上被困人员的位移y＝H－l＝50－(50－t²)＝t²，由此可知，被困人员在竖直方向上做初速度为零、加速度a＝2 m/s²的匀加速直线运动，由牛顿第二定律可得F－mg＝ma，解得悬索的拉力F＝m(g+a)＝600 N.

(2)被困人员5 s末在竖直方向上的速度为v_y＝at＝10 m/s，合速度v＝＝10 m/s，竖直方向上的位移y＝at²＝25 m，水平方向的位移x＝v₀t＝50 m，合位移s＝＝25 m.

(3)t＝5 s时悬索的长度l′＝50－y＝25 m，旋转半径r＝l′sin 37°，

由m＝mgtan 37°，解得v′＝ m/s.此时被困人员B的受力情况如右图所示，

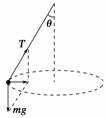
由图可知Tcos 37°＝mg，解得T＝＝625 N.

答案：(1)600 N　(2)10 m/s　25 m　(3)625 N

4.

图4－2－14

如图4－2－14所示，半径为r＝20 cm的两圆柱体A和B，靠电动机带动按相同方向均以角速度ω＝8 rad/s转动，两圆柱体的转动轴互相平行且在同一平面内，转动方向已在图中标出，质量均匀的木棒水平放置其上，重心在刚开始运动时恰在B的正上方，棒和圆柱间动摩擦因数μ＝0.16，两圆柱体中心间的距离s＝1.6 m，棒长l>2 m，重力加速度取10 m/s²，求从棒开始运动到重心恰在A正上方需多长时间？

解析：棒开始与A、B两轮有相对滑动，棒受向左摩擦力作用，做匀加速运动，末速度v＝ωr＝8×0.2 m/s＝1.6 m/s，加速度a＝μg＝1.6 m/s²，时间t₁＝＝1 s，此时间内棒运动位移s₁＝at＝0.8 m．此后棒与A、B无相对运动，棒以v＝ωr做匀速运动，再运动s₂＝AB－s₁＝0.8 m，重心到A正上方时间t₂＝＝0.5 s，故所求时间t＝t₁+t₂＝1.5 s.

答案：1.5 s

3.

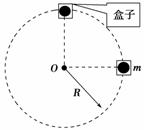
图4－2－13

(2010·湖北部分重点中学联考)如图4－2－13所示，质量为m的小球置于正方体的光滑盒子中，盒子的边长略大于球的直径．某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动，已知重力加速度为g，空气阻力不计，要使在最高点时盒子与小球之间恰好无作用力，则(　)

A．该盒子做匀速圆周运动的周期一定小于2π

B．该盒子做匀速圆周运动的周期一定等于2π

C．盒子在最低点时盒子与小球之间的作用力大小可能小于2mg

D．盒子在最低点时盒子与小球之间的作用力大小可能大于2mg

解析：要使在最高点时盒子与小球之间恰好无作用力，则有mg＝，解得该盒子做匀速圆周运动的速度v＝，该盒子做匀速圆周运动的周期为T＝＝2π.选项A错误，B正确；在最低点时，盒子与小球之间的作用力和小球重力的合力提供小球运动的向心力，由F－mg＝，解得F＝2mg，选项C、D错误．

答案：B

2.

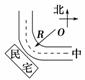
图4－2－12

中央电视台《今日说法》栏目最近报道了一起发生在湖南长沙某区湘府路上的离奇交通事故．

家住公路拐弯处的张先生和李先生家在三个月内连续遭遇了七次大卡车侧翻在自家门口的场面，第八次有辆卡车冲进李先生家，造成三死一伤和房屋严重损毁的血腥惨案．经公安部门和交通部门协力调查，画出的现场示意图如图4－2－12所示．交警根据图示作出以下判断，你认为正确的是(　)

A．由图可知汽车在拐弯时发生侧翻是因为车做离心运动

B．由图可知汽车在拐弯时发生侧翻是因为车做向心运动

C．公路在设计上可能内(东)高外(西)低

D．公路在设计上可能外(西)高内(东)低

解析：由题图可知发生事故时，卡车在做圆周运动，从图可以看出卡车冲入民宅时做离心运动，故选项A正确，选项B错误；如果外侧高，卡车所受重力和支持力提供向心力，则卡车不会做离心运动，也不会发生事故，故选项C正确．

答案：AC

1.

图4－2－11

在观看双人花样滑冰表演时，观众有时会看到女运动员被男运动员拉着离开冰面在空中做水平方向的匀速圆周运动．已知通过目测估计拉住女运动员的男运动员的手臂和水平冰面的夹角约为45°，重力加速度为g＝10 m/s²，若已知女运动员的体重为35 kg，据此可估算该女运动员(　)

A．受到的拉力约为350 N　 　　　　　　 B．受到的拉力约为350 N

C．向心加速度约为10 m/s²　 　　　　 D．向心加速度约为10 m/s²

解析：本题考查了匀速圆周运动的动力学分析．以女运动员为研究对象，受力分析如图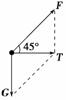．根据题意有G＝mg＝350 N；则由图易得女运动员受到的拉力约为350 N，A正确；向心加速度约为10 m/s²，C正确．

答案：AC

12.

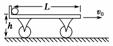
图1－2－11

如图1－2－11所示，一辆上表面光滑的平板小车长L＝2 m，车上左侧有一挡板，紧靠挡板处有一可看成质点的小球．开始时，小车与小球一起在水平面上向右做匀速运动，速度大小为v₀＝5 m/s.某时刻小车开始刹车，加速度a＝4 m/s².经过一段时间，小球从小车右端滑出并落到地面上．求：

(1)从刹车开始到小球离开小车所用的时间；

(2)小球离开小车后，又运动了t₁＝0.5 s落地．小球落地时落点离小车右端多远？

解析：(1)刹车后小车做匀减速运动，小球继续做匀速运动，设经过时间t，小球离开小车，经判断知此时小车没有停止运动，则x_球＝v₀t　 ①

x_车＝v₀t－at² ②

x_球－x_车＝L　 ③

代入数据可解得：t＝1 s　　 ④

(2)经判断小球离开小车又经t₁＝0.5 s落地时，小车已经停止运动．设从刹车到小球落地，小车和小球总位移分别为x₁、x₂，则：x₁＝　 ⑤

x₂＝v₀(t+t₁)　 ⑥

设小球落地时，落点离小车右端的距离为Δx，则：Δx＝x₂－(L+x₁)　　 ⑦

解得：Δx＝2.375 m．⑧

答案：(1)1 s　(2)2.375 m

版权所有：()

版权所有：()

11.

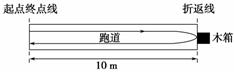
图1－2－10

“10米折返跑”的成绩反应了人体的灵敏素质，如图1－2－10所示．测定时，在平直跑道上，受试者以站立式起跑姿势站在起点终点线前，当听到“跑”的口令后，全力跑向正前方10米处的折返线，测试员同时开始计时，受试者到达折返线处时，用手触摸折返线处的物体(如木箱)，再转身跑向起点终点线，当胸部到达起点终点线的垂直面时，测试员停表，所用时间即为“10米折返跑”的成绩．设受试者起跑的加速度为4 m/s²，运动过程中的最大速度为4 m/s，快到达折返线处时需减速到零，减速的加速度为8 m/s²，返回时达到最大速度后不需减速，保持最大速度冲线．求该受试者“10米折返跑”的成绩为多少秒？

解析：对受试者，由起点终点线向折返线运动的过程中

加速阶段：t₁＝＝1 s，x₁＝v_mt₁＝2 m

减速阶段：t₃＝＝0.5 s；x₃＝v_mt₃＝1 m

匀速阶段：t₂＝＝1.75 s

由折返线向起点终点线运动的过程中

加速阶段：t₄＝＝1 s，x₄＝v_mt₄＝2 m

匀速阶段：t₅＝＝2 s

受试者“10米折返跑”的成绩为：t＝t₁+t₂+…+t₅＝6.25 s.

答案：6.25 s

10．

图1－2－9

(2010·湖北部分重点中学月考)如图1－2－9所示水平传送带A、B两端点相距x＝7 m，起初以v₀＝2 m/s的速度顺时针运转．今将一小物块(可视为质点)无初速度地轻放至A点处，同时传送带以a₀＝2 m/s²的加速度加速运转，已知小物块与传送带间的动摩擦因数为0.4，求：小物块由A端运动至B端所经历的时间．

解析：小物块刚放上传送带时，由牛顿第二定律：μmg＝ma，得：a＝4 m/s²

小物块历时t₁后与传送带速度相同，则：at₁＝v₀+a₀t₁，得：t₁＝1 s

此过程中小物块的位移为：x₁＝at/2，得：x₁＝2 m<x＝7 m

故小物块此时尚未到达B点，且此后的过程中由于a₀<μg，所以小物块将和传送带以共同的加速度运动，设又历时t₂到达B点，则：x－x₁＝at₁t₂+a₀t/2得：t₂＝1 s

小物块从A到B历时：t＝t₁+t₂＝2 s.

答案：2 s

9.

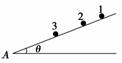
图1－2－8

如图1－2－8所示，在光滑的斜面上放置3个相同的小球(可视为质点)，小球1、2、3距斜面底端A点的距离分别为x₁、x₂、x₃，现将它们分别从静止释放，到达A点的时间分别为t₁、t₂、t₃，斜面的倾角为θ.则下列说法正确的是(　)

A.＝＝　 　　　　　　 B.＞＞

C.＝＝　 　　　　　　 D．若θ增大，则的值减小

解析：三个小球在光滑斜面上下滑时的加速度均为a＝gsin θ，由x＝at²知＝a，因此＝＝.当θ增大，a增大，的值增大，C对，D错.＝，且＝，由物体到达底端的速度v²＝2ax知v₁＞v₂＞v₃，因此₁＞₂＞₃，即＞＞，A错，B对．

答案：BC