3.某同学设计了一个如图所示的实验，将两个斜滑轨道固定在同一竖直面内，其下端水平.把两个质量相等的小钢球从斜面的同一高度由静止释放，滑道2与光滑水平板平滑连接，则他将观察到的现象是　　　　　　　　，这说明　　　　　　　　　.

答案：小球1能击中小球2　平抛运动在水平方向的分运动是匀速运动

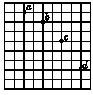
2.在本实验中，为了准确地测出轨迹曲线上各点的坐标并求出初速度，可采取的措施有(　)

A.选距原点近的点测量

B.选距原点远的点测量

C.准确地确定坐标原点和坐标轴

D.准确地测量各点的坐标

答案：BCD

1.在“探究平抛运动的规律”的实验中，如果小球每次从斜槽滚下的初始位置不同，则下列说法中错误的是(　)

A.小球平抛的初速度不同

B.小球每次做不同的抛物线运动

C.小球在空中运动的时间每次均不同

D.小球通过相同的水平位移所用的时间均不同

解析：小球从斜槽上滚下，初始位置不同，则平抛初速度的不同，但不影响竖直方向的运动.

答案：C

13.(14分)图示为一支将要竖直向上发射的火箭，其质量为6000 kg，点火后喷气速度为2.5 km/s，忽略发射初期火箭质量的变化，问：(取g＝10 m/s²)

(1)点火后每秒至少要喷射多少气体才能使火箭开始上升？

(2)如果要使火箭开始有2 m/s²向上的加速度，则每秒要喷出多少气体？

解析：(1)设火箭每秒喷射出质量为m₀的高速气体时产生的反冲力大小等于火箭的重力.对于Δt时间的喷出的气体，由动量定理得：

F·Δt＝m₀·Δt·v₀－0

由牛顿第三定律得：F＝Mg＝60000 N

解得：m₀＝24 kg.

(2)设每秒喷出质量为m的气体时能使火箭以2 m/s²的加速度加速上升，则此时火箭受到的冲力大小为：

F′＝Mg+ma＝7.2×10⁴ N

对于Δt时间内喷出的气体，由动量定理得：

F′·Δt＝m·Δt·v₀－0

解得：m＝28.8 kg.

答案：(1)24 kg　(2)28.8 kg

12.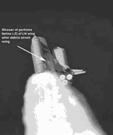(13分)关于哥伦比亚号航天飞机失事的原因，美国媒体报道说，航天飞机发射时一块脱落的泡沫损伤了左翼的隔热瓦，于是最终酿成大祸.据美国航天局航天计划的Dittemore于2003年2月5日在新闻发布会上说，撞击航天飞机左翼的泡沫长20英寸(约50.8 cm)、宽16英寸(约40.6 cm)、厚6英寸(约15.2 cm)，其质量大约为1.3 kg，撞击时速度约为250 m/s，方向向上，而航天飞机的上升速度大约为700 m/s.假定碰撞时间等于航天飞机前进泡沫的长度所用的时间，相撞后认为泡沫全部附在飞机上.根据以上信息，估算“哥伦比亚”号航天飞机左翼受到的平均撞击力.(结果保留一位有效数字)

解析：由题意知航天飞机与泡沫块的作用时间为：

Δt＝ s

设碰撞过程中航天飞机对泡沫块的平均冲力大小为F，由动量定理得：

F·Δt＝mv₁－mv₂　(F远大于泡沫块受的重力)

解得：F＝8×10⁵ N

由牛顿第三定律知，航天飞机左翼受到的平均撞击力为8×10⁵ N.

答案：8×10⁵ N

11.(13分)某中学生身高1.80 m，质量70 kg.他站立举臂，手指摸到的高度为2.25 m.如果他先缓慢下蹲，再用力蹬地向上跳起，同时举臂，手指摸到的高度为2.70 m.设他从蹬地到离开地面所用的时间为0.3 s.取g＝10 m/s²，求：

(1)他刚离地跳起时的速度大小.

(2)他与地面间的平均作用力的大小.

解析：(1)跳起后重心升高

h＝2.70 m－2.25 m＝0.45 m.

根据机械能守恒定律mv²＝mgh　

解得：v＝＝3 m/s.

(2)根据动量定理有：(F－mg)t＝mv－0

解得：F＝m(g+)＝1400 N.

答案：(1)3 m/s　(2)1400 N

10.如图所示，一个下面装有轮子的贮气瓶停放在光滑的水平地面上，底端与竖直墙壁接触.现打开右端阀门，气体向外喷出，设喷口的面积为S，气体的密度为ρ，气体向外喷出的速度为v，则气体刚喷出时钢瓶底端对竖直墙面的作用力大小是(　)

A.ρvS　　B.　　C.ρv²S　　D.ρv²S

解析：Δt时间内气瓶喷出气体的质量Δm＝ρSv·Δt

对于贮气瓶、瓶内气体及喷出的气体所组成的系统，由动量定理得：

F·Δt＝Δm·v－0

解得：F＝ρv²S，选项D正确.

答案：D

非选择题部分共3小题，共40分.

9.水平拉力F₁、F₂分别作用在水平面的物体上一段时间后又撤去，使物体都由静止开始运动而后又停下.如果物体在两种情况下的总位移相等，且F₁＞F₂，那么在这样的情况中(　)

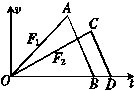A.F₁比F₂的冲量大

B.F₁比F₂的冲量小

C.F₁与F₂的冲量相等

D.F₁与F₂的冲量大小无法比较

解析：

在同一图中作出两种情况下的v－t图象.在物体做减速运动的阶段，由于动摩擦因数相同，故加速度相等，图中CD平行于AB.因为F₁＞F₂，所以物体受F₁作用时比受F₂作用时的加速度大.物体两次通过的总位移相等，表明△AOB与△COD的面积相等.

设F₁、F₂的作用时间和它们撤去后物体滑行的时间分别为t₁、t₂、t₁′、t₂′，物体的始末动量均为零，根据动量定理有：

F₁t₁－f(t₁+t₁′)＝0

F₂t₂－f(t₂+t₂′)＝0

由图可知：t₁+t₁′＜t₂+t₂′，所以f(t₁+t₁′)＜f(t₂+t₂′)

即F₁t₁＜F₂t₂，故选项B正确.

答案：B

8.光子有能量也有动量，动量p＝，它也遵守有关动量的规律.如图所示，在真空中，有一“∞”字形装置可绕通过横杆中点的竖直轴OO′在水平面内灵活地转动，其中左边是圆形黑纸片(吸收光子)，右边是和左边大小、质量均相同的圆形白纸片(反射光子).当用平行白光垂直照射这两个圆面时，关于装置开始转动时的情况(俯视)，下列说法中正确的是(　)

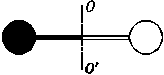
A.顺时针方向转动

B.逆时针方向转动

C.都有可能

D.不会转动

解析：一个光子与白纸片碰撞的过程I_右＝2p_光；一个光子与黑纸片碰撞的过程I_左＝p_光；故I_右＞I_左，选项B正确.

答案：B

7.

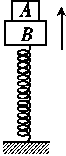如图所示，竖直放置的轻弹簧，一端固定于地面，另一端与质量为3 kg的物体B固定在一起，质量为1 kg的物体A放于B上，现在A和B一起竖直向上运动.当A、B分离后，A上升0.2 m到达最高点，此时B的速度方向向下，弹簧为原长，则从A、B分离起至A到达最高点的过程中，弹簧的弹力对B的冲量大小为(g取10 m/s²)(　)

A.1.2 N·s　 B.8 N·s

C.6 N·s　 D.4 N·s

解析：A、B在弹簧为原长时的位置分离，由题意知此时A、B的速度v₀＝＝2 m/s.过原长位置后，由于加速度、速度不同而使A上升，上升的时间为：Δt＝＝0.2 s，A、B分离，对于B有：

I_弹+mgΔt＝mv₀－m(－v₀)＝2mv₀

代入数据解得：I_弹＝6 N·s，选项C正确.

答案：C