
题目列表(包括答案和解析)
5. 一根轻杆,左端O为转轴,a、b、c为三个质量相等的小球,均匀固定在杆上(即Oa=ab=bc),轻杆带动三个小球在水平面是做匀速转动,如图所示。则三段杆的张力之比T1:T2:T3
 A、1:2:3
B、3:2:1
A、1:2:3
B、3:2:1
C、6:5:3 D、6:5:2
4. 一列简谐波沿直线传播,在波的传播方向上,介质中有P、Q两质点相距6m。在t=0时刻,P、Q同时反向经过平衡位置,且中间只有一个波峰,而在t=0.1s时刻,P、Q又同时经过平衡位置,则这列波的波长和波速可能是:
A、 2m,60m/s;
B、 4m,20m/s;
C、 6m,30m/s;
D、 3m,15m/s。
3. 如图(a)、(b)所示,并排放在光滑水平面上的物体P、Q质量分别为M、m,大小为F的水平推力作用于P时,P、Q间作用力大小为N1,同样大小的水平推力F作用于Q上时,P、Q间的作用力大小为N2。则
A、 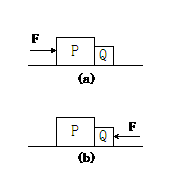 N1
=N2
N1
=N2
B、 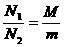
C、 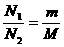
D、 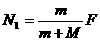
2. 在同一匀强电场中,两带电粒子只受电场力作用,
A、 其中带电量大的,其加速度一定大;
B、 若两粒子质量相等,它们加速度大小必相等;
C、 粒子的荷质比相等,它们的加速度就相等;
D、 粒子的荷质比相等,它们的加速度也可能不相等;
一个力学的金科玉律-牛顿第二运动定律
|
例如以上各种运动的受力特点:
(1)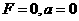 …………………………………物体静止或作匀速直线运动(平衡状态)
…………………………………物体静止或作匀速直线运动(平衡状态)
这也是从实验方法验证牛顿第一运动定律(理想定律)的思路。
(2)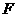 恒定,
恒定,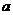 也恒定,而且
也恒定,而且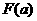 与
与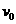 同一直线………………物体做匀变速直线运动
同一直线………………物体做匀变速直线运动
(3)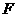 恒定,
恒定,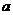 也恒定,而且
也恒定,而且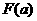 与
与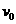 不同直线……………… 物体做匀变速曲线运动
不同直线……………… 物体做匀变速曲线运动
(4)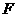 大小不变而方向始终垂直
大小不变而方向始终垂直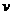 指向圆心…………………………物体做匀速圆周运动
指向圆心…………………………物体做匀速圆周运动
(5)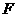 与位移
与位移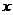 的关系为
的关系为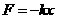 (回复力)
(回复力)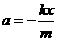 …………………物体做简谐运动
…………………物体做简谐运动
附:一个使物体产生转动效果的物理量--力矩
公式: 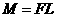
单位: 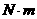 (不能化成
(不能化成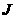 )
)
规定: 能使物体产生逆时针转动的为正力矩
能使物体产生顺时针转动的为负力矩
[一般解题思路]

[例题选讲]
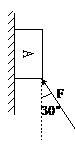
[例1]重力为G的物体A受到与竖直方向成α角的外力F后,静止在竖直墙面上,如图所示,试求墙对物体A的静摩擦力。
解析:当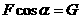 时,物体在竖直方向上受力已经平衡,故静摩擦力为零;
时,物体在竖直方向上受力已经平衡,故静摩擦力为零;
当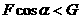 时,物体有向下滑动的趋势,故静摩擦力f的方向向上,大小为
时,物体有向下滑动的趋势,故静摩擦力f的方向向上,大小为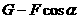 ;
;
当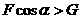 时,物体有向上滑动的趋势,故静摩擦力f的方向向下,大小为
时,物体有向上滑动的趋势,故静摩擦力f的方向向下,大小为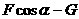 。
。

[例2]竖直绝缘壁上的Q点有一固定的质点A,在Q的正下方P点用丝线悬挂另一质点B,已知PA=PB,A、B两质点因带电而互相排斥,致使悬线和竖直方向成θ角,(如图所示),由于漏电使A、B两质点的带电量逐渐减少,在电荷漏完之前悬线对悬点P的拉力大小。
A、逐渐减小 B、逐渐增大
C、保持不变 D、先变小后变大
解析:质点B受重力G、悬线的拉力T和静电场力F三力作用而平衡,这三力中,T与F的大小、方向均随θ角的变化而变化。由F合、T、F三力构成的三角形与几何三角形PAB相似,所以有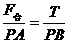 。又∵F合=G,解之得:
。又∵F合=G,解之得: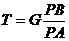 ,由于在θ减小过程中,PA与PB相等,故T始终与G相等,可见,悬线对悬点P的拉力大小保持不变,选项C正确。
,由于在θ减小过程中,PA与PB相等,故T始终与G相等,可见,悬线对悬点P的拉力大小保持不变,选项C正确。
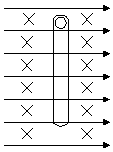 [例3]如图所示,在绝缘的竖直放置的塑料管内有一质量为0.1g、带电量
[例3]如图所示,在绝缘的竖直放置的塑料管内有一质量为0.1g、带电量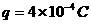 的小球,管子放在如图所示的正交匀强电场和匀强磁场中。匀强电场方向水平向右,匀强磁场的方向垂直于纸面向里。已知磁感应强度B=0.5T,电场强度E=10N/C,小球与管壁间的动摩擦因数μ=0.2,g取10m/s2,管子足够长。求:
的小球,管子放在如图所示的正交匀强电场和匀强磁场中。匀强电场方向水平向右,匀强磁场的方向垂直于纸面向里。已知磁感应强度B=0.5T,电场强度E=10N/C,小球与管壁间的动摩擦因数μ=0.2,g取10m/s2,管子足够长。求:
(1)小球沿管子内壁下滑的最大速度;
(2)若其他条件不变,仅将电场方向反向时,小球下滑的最大速度。
 解:(1)开始时,小球速度为零,受到重力、电场力和管壁的弹力和摩擦力,一旦小球向下运动,小球除了受到上述四个力的作用外还受到洛伦兹力。小球从静止开始向下加速运动,随着速度的增加,洛伦兹力
解:(1)开始时,小球速度为零,受到重力、电场力和管壁的弹力和摩擦力,一旦小球向下运动,小球除了受到上述四个力的作用外还受到洛伦兹力。小球从静止开始向下加速运动,随着速度的增加,洛伦兹力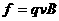 随着增大,压力
随着增大,压力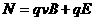 也逐渐增大,滑动摩擦力
也逐渐增大,滑动摩擦力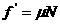 也逐渐增大,而重力和电场力是不变的,故小球加速度渐减。当加速度减为零,即小球受力平衡是速度最大,此时小球受力如图(1)所示。由于
也逐渐增大,而重力和电场力是不变的,故小球加速度渐减。当加速度减为零,即小球受力平衡是速度最大,此时小球受力如图(1)所示。由于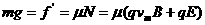 ,得
,得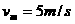 。
。
(2)在电场方向反向的情况下,由于洛伦兹力同电场力反向,当速度逐渐增大时,洛伦兹力渐增,压力渐减,摩擦力渐减,加速度渐增。当电场力和洛伦兹力平衡时,摩擦力为零,加速度最大为a=g。随着小球速度继续增加,洛伦兹力大于电场力,压力反向并逐渐增大,摩擦力又逐渐增大,加速度逐渐减少直至为零。此时小球受力平衡,速度达到最大,小球受力如图(2)所示,由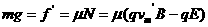 ,得
,得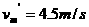 。
。
[练习题]
1. 竖直向上抛出的小球,运动中所受的空气阻力不能忽略。则
A、 因为小球向上做减速运动,向下做加速运动,所以小球向上的加速度小于向下的加速度;
B、 小球向上运动时所受合力大于向下运动时的合力;
C、 小球到达最高点时的加速度为零;
D、 小球到达最高点时的加速度为g(重力加速度)。
8、 如图所示,电源E=2V,r=0. 5欧,竖直导轨电阻可忽略,金属棒的质量m=0.1㎏,电阻R=0.5欧,它与导轨间的动摩擦因素μ=0.4,有效长度为L=0.2m,水平的靠在导轨的外侧面,为了使金属棒不滑动,我们加一与纸面成30°向里的匀强磁场B,求;(1)此磁场是斜向上还是斜向下?(2)B的大小在什么范围内?
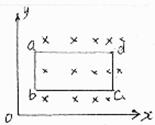
7、如图所示,矩形线圈边长ab=5cm,ad=10cm,电阻为2Ω。磁场方向垂直线圈平面,磁感应强度沿正x轴均匀增加,且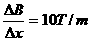 ,若使线圈沿正x方向以v=2m/s的速度匀速运动,运动中ab边始终与y轴平行。求运动过程中水平拉力的功率。
,若使线圈沿正x方向以v=2m/s的速度匀速运动,运动中ab边始终与y轴平行。求运动过程中水平拉力的功率。
6、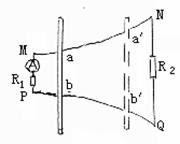 图为两根间距不等的光滑金属导轨MN、PQ,它们水平放置在竖直向下的匀强磁场中。导轨的一端接入电阻R1=10Ω和电流表,另一端接入电阻R2=5Ω。质量为m=0.1kg的金属棒横放在导轨上。当它以初速度v0=4m/s从ab处滑到a′b′处,同时t=0.08s。导轨间距Lab=0.4m,L a′b′=0.8m。若金属滑动时电流表读数始终不变。不计电流表棒与导轨的电阻和摩擦。试求:
图为两根间距不等的光滑金属导轨MN、PQ,它们水平放置在竖直向下的匀强磁场中。导轨的一端接入电阻R1=10Ω和电流表,另一端接入电阻R2=5Ω。质量为m=0.1kg的金属棒横放在导轨上。当它以初速度v0=4m/s从ab处滑到a′b′处,同时t=0.08s。导轨间距Lab=0.4m,L a′b′=0.8m。若金属滑动时电流表读数始终不变。不计电流表棒与导轨的电阻和摩擦。试求:
(1)电流表的读数;
(2)磁感应强度。
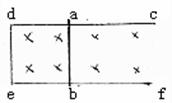
5、如图所示,固定于水平桌面上的金属框架cdef处于竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动,此时abed构成一个边长为L的正方形。棒的电阻为r,其余部分电阻不计。开始时磁感应强度为B0。
(1)若从t=0时刻起,磁感应强度均匀增加,每秒增量为K,同时保持棒静止,求棒中的感应电流,并指明其方向。
(2)在上述(1)的情况中,始终保持棒静止,当t=t1秒末时,需加的垂直于棒的水平拉力为多大?
(3)若从t=0时记刻起,磁感应强度逐渐减小,当棒以恒定速度v向右作匀速运动时 可使棒中不产生感应电流,则磁感应强度应怎样随时间变化?(写出B与t的关系式)
4、 核聚变反应需要几百万度以上的高温,为把高温条件下高速运动的离子约束在小范围内(否则不可能发生核反应),通常采用磁约束的方法(托卡马克装置)。如图11一19所示,环状匀强磁场围成中空区域,中空区域中的带电粒子只要速度不是很大,都不会穿出磁场的外边缘而被约束在该区域内。设环状磁场的内半径为R1=0.5m,外半径R2=1.0m,磁场的磁感强度B=1.0T,若被束缚带电粒子的荷质比为q/m=4×107c/㎏,中空区域内带电粒子具有各个方向的速度。试计算
核聚变反应需要几百万度以上的高温,为把高温条件下高速运动的离子约束在小范围内(否则不可能发生核反应),通常采用磁约束的方法(托卡马克装置)。如图11一19所示,环状匀强磁场围成中空区域,中空区域中的带电粒子只要速度不是很大,都不会穿出磁场的外边缘而被约束在该区域内。设环状磁场的内半径为R1=0.5m,外半径R2=1.0m,磁场的磁感强度B=1.0T,若被束缚带电粒子的荷质比为q/m=4×107c/㎏,中空区域内带电粒子具有各个方向的速度。试计算
(1)粒子沿环状的半径方向射入磁场,不能穿越磁场的最大速度。
(2)所有粒子不能穿越磁场的最大速度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com