
题目列表(包括答案和解析)
14.天文学家测得银河系中氦的含量约为25%.有关研究表明,宇宙中氮生成的途径有两条:一是在宇宙诞生后2 min左右生成的;二是在宇宙演化到恒星诞生后,由恒星内部的氢核聚变反应生成的.
(1)把氢核聚变简化为4个氢核(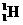 )聚变成氦核
)聚变成氦核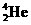 ,同时放出2个正电子(
,同时放出2个正电子(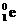 )和2个中微子(
)和2个中微子(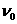 ),请写出该氢核聚变反应的方程,并计算一次反应释放的能量.
),请写出该氢核聚变反应的方程,并计算一次反应释放的能量.
(2)研究表明,银河系的年龄约为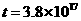 s,每秒银河系产生的能量约为
s,每秒银河系产生的能量约为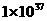 J
J 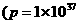 J/s),现假定该能量全部来自上述氢核聚变反应,试估算银河系中氦的含量(最后结果保留一位有效数字)
J/s),现假定该能量全部来自上述氢核聚变反应,试估算银河系中氦的含量(最后结果保留一位有效数字)
(3)根据你的估算结果,对银河系中氦的主要生成途径作出判断.
可能用到的数据:银河系的质量约为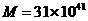 kg,原子质量单位
kg,原子质量单位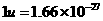 kg, l u相当于
kg, l u相当于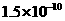 J的能量,电子质量m=0. 000 5 u,氦核质量
J的能量,电子质量m=0. 000 5 u,氦核质量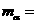 =4.002 6 u,氢核质量
=4.002 6 u,氢核质量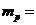 1. 008 7 u,中微子
1. 008 7 u,中微子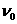 质量为零.
质量为零.
解析:(1)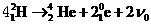 ,
,
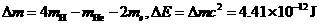
(2)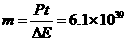 kg
kg
氦的含量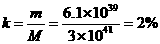
(3)由估算结果可知,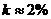 远小于25%的实际值,所以银河系中氦的主要是宇宙诞生后不久生成的。
远小于25%的实际值,所以银河系中氦的主要是宇宙诞生后不久生成的。
13.在用铀235作燃料的核反应堆中,铀235核吸收一个动能约为0.025 eV的热中子(慢中子)后,可发生裂变反应.放出能量和2-3个快中子,而快中子不利于铀235的裂变.为了能使裂变反应继续下去,需要将反应中放出的快中子减速.有一种减速的方法是使用石墨(碳12)作减速剂.设中子与碳原子的碰撞是对心弹性碰撞,问一个动能为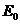 =1. 75 MeV的快中子需要与静止的碳原子碰撞多少次,才能减速成为0. 025 eV的热中子?(可能用到的数据
=1. 75 MeV的快中子需要与静止的碳原子碰撞多少次,才能减速成为0. 025 eV的热中子?(可能用到的数据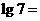 0. 84,
0. 84,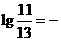 0.073)
0.073)
解析:设中子和碳核的质量分别为 和
和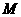 ,碰撞前中子的速度为
,碰撞前中子的速度为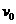 ,碰撞后中子和碳核的速度分别为
,碰撞后中子和碳核的速度分别为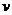 和
和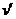 ,因为碰撞是弹性碰撞,所以在碰撞前后,动量和机械能均守恒,又因为
,因为碰撞是弹性碰撞,所以在碰撞前后,动量和机械能均守恒,又因为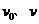 和
和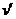 沿同一直线,故有
沿同一直线,故有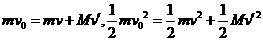
解上两式得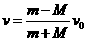
因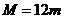 得
得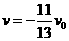
负号表示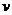 的方向与
的方向与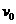 方向相反,即与碳核碰撞后中子被反弹.因此,经过一次碰撞后中子的能量为
方向相反,即与碳核碰撞后中子被反弹.因此,经过一次碰撞后中子的能量为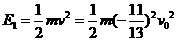 ,于是
,于是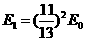
经过2,3,…n次碰撞后,中子的能量依次为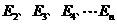 ,有
,有
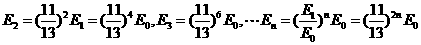 ,
,
因此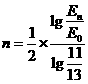
已知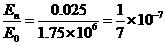
得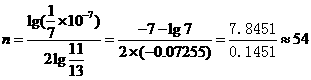
故初能量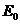 =1. 75 MeV的快中子经过近54次碰撞后,才成为能量为0. 025 eV的热中子。
=1. 75 MeV的快中子经过近54次碰撞后,才成为能量为0. 025 eV的热中子。
12.如图所示,某一足够大的真空中,虚线PH右侧是磁感应强度为B、方向垂直于纸面向里的匀强磁场,左侧是一场强为E、方向水平向左的匀强电场.静止于虚线 PH上的一点O处的镭核(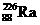 )水平向右放出一个
)水平向右放出一个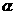 粒子而衰变成氡核(
粒子而衰变成氡核(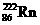 ).设
).设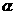 粒子与氡核分离后它们之间的作用可忽略不计,涉及动量问题时亏损的质量不计,重力不计.
粒子与氡核分离后它们之间的作用可忽略不计,涉及动量问题时亏损的质量不计,重力不计.
(1)写出镭核衰变的核反应方程.
(2)若经过一段时间,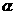 粒子刚好到达虚线PH上的A点,测得OA=L,求此时氡核的速率(已知
粒子刚好到达虚线PH上的A点,测得OA=L,求此时氡核的速率(已知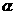 粒子的比荷为b)
粒子的比荷为b)
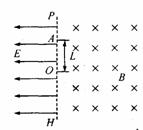
解析:(1)镭衰变的核反应方程为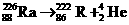
(2)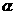 粒子进入匀强磁场后做匀速圆周运动
粒子进入匀强磁场后做匀速圆周运动
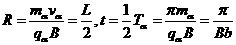
衰变时,根据动量守恒有: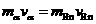
所以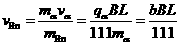
氡在电场中做匀加速运动且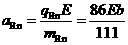
所以: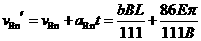 。
。
11.19世纪50年代人们发现氢原子光谱中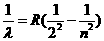 (R为一常量,n=3、4、5…),物理学家玻尔在他28岁时连续发表三篇论文,成功地解释了氢原子光谱的规律,揭示了光谱线与原子结构的内在联系,玻尔理论是从经典理论向量子理论的一个重要过渡,为量子力学的诞生提供了条件.玻尔既引入量子化的概念,同时又运用了“轨道”等经典物理理论和牛顿力学的规律推导出上述公式.请同学们试用课本知识和以下假设定量做玻尔的推导.(1)绕氢原子核旋转的电子质量为m,电量为-e;(2)取离核无限远处的电势能为零,半径r处电子的电势能为
(R为一常量,n=3、4、5…),物理学家玻尔在他28岁时连续发表三篇论文,成功地解释了氢原子光谱的规律,揭示了光谱线与原子结构的内在联系,玻尔理论是从经典理论向量子理论的一个重要过渡,为量子力学的诞生提供了条件.玻尔既引入量子化的概念,同时又运用了“轨道”等经典物理理论和牛顿力学的规律推导出上述公式.请同学们试用课本知识和以下假设定量做玻尔的推导.(1)绕氢原子核旋转的电子质量为m,电量为-e;(2)取离核无限远处的电势能为零,半径r处电子的电势能为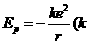 为静电力常量);(3)电子所在的轨道的圆周长与其动量的乘积等于普朗克常量h的整数倍时,这样的轨道才是电子的可能轨道.
为静电力常量);(3)电子所在的轨道的圆周长与其动量的乘积等于普朗克常量h的整数倍时,这样的轨道才是电子的可能轨道.
解析:设氢原子核外电子的速度为v,可能的轨道半径为r,则有
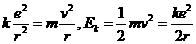
所以核外电子的总能量为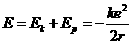
由题意知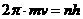 ,故
,故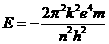
由玻尔的跃迁理论有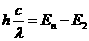 ,
,
即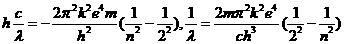
故巴耳末线系的波长符合公式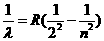 。
。
10.某实验室工作人员,用初速度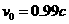 (c为真空中的光速)的
(c为真空中的光速)的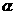 粒子,轰击静止的氮原子核
粒子,轰击静止的氮原子核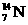 ,产生了质子
,产生了质子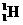 。若某次碰撞可看作对心正碰,碰后新核与质子同方向运动,垂直磁场方向射入磁场,通过分析偏转半径可得出新核与质子的速度大小之比为1:20,已知质子质量为m。
。若某次碰撞可看作对心正碰,碰后新核与质子同方向运动,垂直磁场方向射入磁场,通过分析偏转半径可得出新核与质子的速度大小之比为1:20,已知质子质量为m。
(1)写出核反应方程.
(2)求出质子的速度v.
(3)若用上述两个质子发生对心弹性碰撞,则每个质子的动量变化量是多少?(保留两位有效数字)
解析:(1)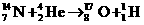
(2)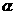 粒子、新核的质量分别为4m、17m,质子的速度为v,对心正碰,有
粒子、新核的质量分别为4m、17m,质子的速度为v,对心正碰,有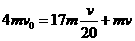 ,得
,得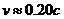
(3)质量相等且弹性碰撞,交换速度.对某一质子,选其末动量方向为正方向,则
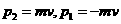 ,又
,又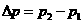
故解出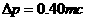 ,方向与末动量方向一致.
,方向与末动量方向一致.
9.太阳的能量来自下面的反应:四个质子(氢核)聚变成一个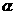 粒子,同时发射两个正电子和两个没有静止质量的中微子,若太阳辐射能量的总功率为P,质子
粒子,同时发射两个正电子和两个没有静止质量的中微子,若太阳辐射能量的总功率为P,质子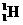 。氦核
。氦核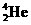 、正电子
、正电子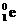 的质量分别为
的质量分别为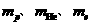 ,真空中的光速为c,求:
,真空中的光速为c,求:
(1)写出核反应方程式。
(2)核反应所释放的能量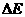 。
。
(3)在t时间内参与上述热核反应的质子数目。
解析:(1)核反应方程式为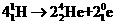
(2)质量亏损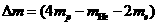 ,根据爱因斯坦质能方程得
,根据爱因斯坦质能方程得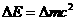 ,核反应释放的能量
,核反应释放的能量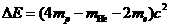
(3)设时间t内参与热核反应的质子数为N
依据能量关系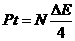 有
有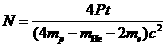 。
。
8.静止的锂核(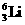 ))俘获一个速度为
))俘获一个速度为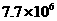 m/s的中子,发生核反应后若只产生了两个新粒子,其中一个粒子为氦核(
m/s的中子,发生核反应后若只产生了两个新粒子,其中一个粒子为氦核(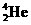 ),它的速度大小是
),它的速度大小是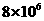 m/s,方向与反应前的中子速度方向相同.
m/s,方向与反应前的中子速度方向相同.
(1)写出此核反应的方程式;
(2)求反应后产生的另一个粒子的速度大小及方向;
(3)此反应过程中是否发生了质量亏损,说明依据.
解析:(1)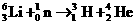
(2)用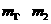 和
和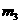 分别表示中子(
分别表示中子(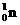 )、氦核(
)、氦核(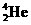 )和氚核(
)和氚核(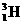 )的质量,用
)的质量,用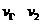 和
和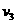 分别表示中子、氦核和氚核的速度,由动量守恒定律得
分别表示中子、氦核和氚核的速度,由动量守恒定律得
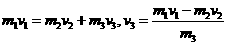
代入数值,得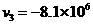 m/s
m/s
即反应后生成的氚核的速度大小为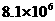 m/s,方向与反应前中子的速度方向相反
m/s,方向与反应前中子的速度方向相反
(3)反应前的总动能为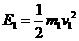
反应后的总动能为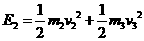
经计算知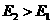 .故反应过程中发生了质量亏损失
.故反应过程中发生了质量亏损失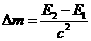 。
。
7.静止在匀强磁场中的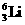 核俘获一个运动方向垂直于磁场,速度大小为
核俘获一个运动方向垂直于磁场,速度大小为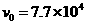 m/s的中子,发生核反应
m/s的中子,发生核反应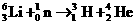 .若已知
.若已知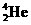 核的速度大小为
核的速度大小为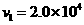 m/s,方向与反应前中子的速度方向相同,求:
m/s,方向与反应前中子的速度方向相同,求:
(1)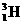 核的速度;
核的速度;
(2)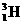 核与
核与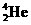 核在磁场中做匀速圆周运动的半径之比;
核在磁场中做匀速圆周运动的半径之比;
(3)当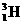 核旋转3周时,
核旋转3周时,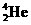 核旋转几周?
核旋转几周?
解析:(1)由动量守恒定律,有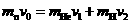
解得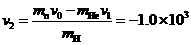 m/s
m/s
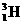 核的速度大小为
核的速度大小为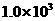 m/s,方向与中子的运动方向相反.
m/s,方向与中子的运动方向相反.
(2)粒子做匀速圆周运动的半径为R,由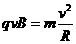 ,得
,得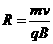 。则
。则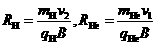 ,得
,得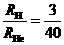
(3)粒子做匀速圆周运动的周期为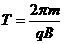 ,则
,则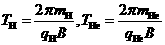 ,得
,得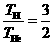
所以,当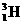 核旋转3周时,
核旋转3周时,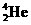 核旋转2周。
核旋转2周。
6.一静止的质量为M的氡核(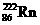 )发生
)发生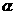 衰变,放出一个速度为
衰变,放出一个速度为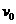 、质量为m的
、质量为m的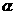 粒子和一个反冲核钋(Po),若氡核发生衰变时,释放的能量全部转化为
粒子和一个反冲核钋(Po),若氡核发生衰变时,释放的能量全部转化为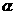 粒子和钋核的动能.
粒子和钋核的动能.
(1)写出衰变方程;
(2)求出衰变过程中的质量亏损(亏损的质量在与粒子质量相比时可忽略不计).
解析:(1)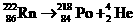
(2)设钋核反冲速度大小为v,由动量守恒定律得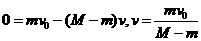
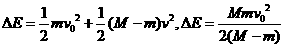
由爱因斯坦质能方程,得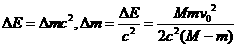 。
。
5.在真空中,原来静止的原子核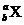 在进行
在进行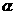 衰变时,放出
衰变时,放出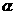 粒子的动能为
粒子的动能为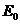 。假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计.
。假设衰变后产生的新核用字母Y表示,衰变时产生的能量全部以动能形式释放出来,真空中的光速为c,原子核的质量之比等于质量数之比,原子核的重力不计.
(1)写出衰变的核反应方程;
(2)求衰变过程中总的质量亏损.
解析:(1)衰变的核反应方程为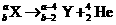
(2)根据动量守恒定律,反冲核Y的动量与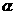 粒子的动量大小相等.由
粒子的动量大小相等.由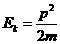 知,反冲核Y的动能为
知,反冲核Y的动能为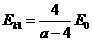
衰变时释放出的总能量为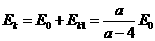
报据爱因斯坦的质能方程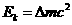
此衰变过程中总的质量亏损是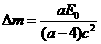 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com