
题目列表(包括答案和解析)
3.(2008年浙江省绍兴市)如图,沿虚线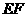 将
将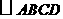 剪开,则得到的四边形
剪开,则得到的四边形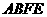 是( )
是( )
A.梯形 B.平行四边形 C.矩形 D.菱形

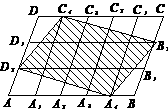
1. (2008年山东省潍坊市)在平行四边形ABCD中,点A1、A2、A3、A4和C1、C2、C3、C4分别AB和CD的五等分点,点B1、B2、B3和D1、D2、D3分别是BC和DA的三等分点,已知四边形A4 B2 C4 D2的积为1,则平行四边形ABCD面积为( )
A.2 B.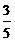 C.
C.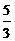 D.15
D.15
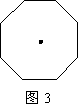
2(2008年辽宁省十二市)图3是对称中心为点 的正八边形.如果用一个含
的正八边形.如果用一个含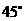 角的直角三角板的角,借助点
角的直角三角板的角,借助点 (使角的顶点落在点
(使角的顶点落在点 处)把这个正八边形的面积
处)把这个正八边形的面积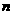 等分.那么
等分.那么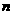 的所有可能的值有( )
的所有可能的值有( )
A.2个 B.3个 C.4个 D.5个
24. 解:(1)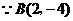 在
在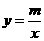 上
上
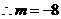 .
.
 反比例函数的解析式为:
反比例函数的解析式为: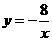 .······························· 1分
.······························· 1分
 点
点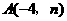 在
在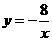 上
上
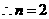
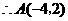 ···················································································································· 2分
···················································································································· 2分
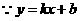 经过
经过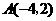 ,
,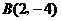 ,
,
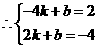
解之得
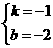
 一次函数的解析式为:
一次函数的解析式为: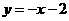 ············································································· 4分
············································································· 4分
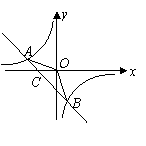 (2)
(2) 是直线
是直线 与
与 轴的交点
轴的交点
 当
当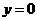 时,
时,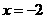
 点
点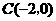 ……………………………………………5分
……………………………………………5分
 …………………………………………………………6分
…………………………………………………………6分
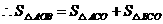
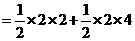
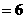 8分
8分
23.
解:(1)将点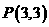 代入
代入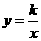 中,得k=9;
中,得k=9;
(2) 设Q点的纵坐标为y,则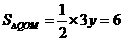 ,解得:y=4
,解得:y=4
将y=4,k=9代入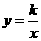 中,得
中,得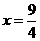 .
. Q
Q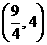
22.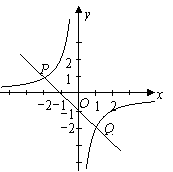 解:(1)设反比例函数关系式为
解:(1)设反比例函数关系式为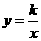 ,
,
 反比例函数图象经过点
反比例函数图象经过点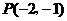 .
.
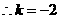 .···························································· 2分
.···························································· 2分
 反比例函数关第式
反比例函数关第式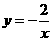 .······························ 3分
.······························ 3分
(2) 点
点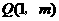 在
在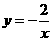 上,
上,
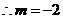 .·················································································································· 5分
.·················································································································· 5分
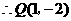 .················································································································ 6分
.················································································································ 6分
(3)示意图.·············································································································· 8分
当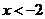 或
或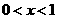 时,一次函数的值大于反比例函数的值.···································· 10分
时,一次函数的值大于反比例函数的值.···································· 10分
21. 21.(1)∵ A(m,3)与B(n,2)关于直线y = x对称,
∴ m = 2,n = 3, 即 A(2,3),B(3,2).
于是由 3 = k∕2,得 k = 6. 因此反比例函数的解析式为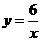 .
.
(2)设过B、D的直线的解析式为y = kx + b.
∴ 2
= 3k + b,且 -2 = 0 · k + b. 解得k =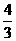 ,b =-2.
,b =-2.
故直线BD的解析式为 y =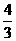 x-2.
x-2.
∴ 当y = 0时,解得 x = 1.5.
即 C(1.5,0),于是 OC = 1.5,DO = 2.
在Rt△OCD中,DC =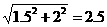 .
.
∴ sin∠DCO =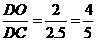 .
.
说明:过点B作BE⊥y轴于E,则 BE = 3,DE = 4,从而 BD = 5,sin∠DCO = sin∠DBE =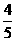 .
.
20. 解:(1)设所求反比例函数的解析式为: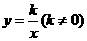 .
.
 点
点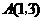 在此反比例函数的图象上,
在此反比例函数的图象上,
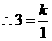 ,
,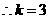 .
.
故所求反比例函数的解析式为: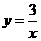 .
.
(2)设直线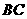 的解析式为:
的解析式为: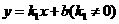 .
.
 点
点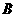 的反比例函数
的反比例函数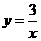 的图象上,点
的图象上,点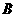 的纵坐标为1,设
的纵坐标为1,设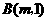 ,
,
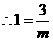 ,
,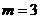 .
.
 点
点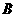 的坐标为
的坐标为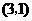 .
.
由题意,得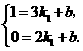
解得: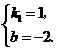
 直线
直线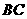 的解析式为:
的解析式为: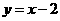 .
.
19.
解:(1)解方程组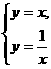 得,
得,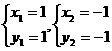
所以A、B两点的坐标分别为:A(1,1)、B(-1,-1)
(2)根据图象知,当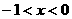 或
或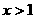 时,正比例函数值大于反比例函数值
时,正比例函数值大于反比例函数值
18.
解:(1) ∵双曲线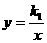 过点
过点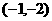
∴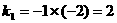
∵双曲线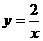 过点
过点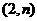
∴
 由直线
由直线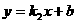 过点
过点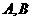 得
得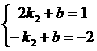 ,解得
,解得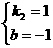
∴反比例函数关系式为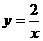 ,一次函数关系式为
,一次函数关系式为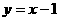 .
.
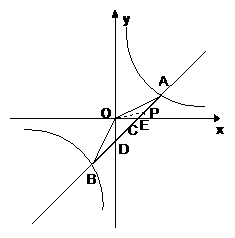
(2)存在符合条件的点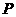 ,
,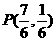 .理由如下:
.理由如下:
∵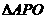 ∽
∽
∴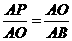 ∴
∴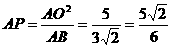 ,如右图,设直线
,如右图,设直线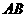 与
与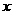 轴、
轴、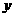 轴分别相交于点
轴分别相交于点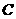 、
、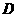 ,过
,过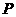 点作
点作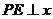 轴于点
轴于点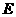 ,连接
,连接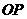 ,则
,则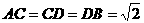 ,
,
故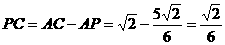 ,再由
,再由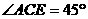 得
得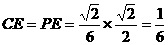 ,从而
,从而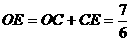 ,因此,点
,因此,点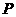 的坐标为
的坐标为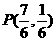 .
.
17. 解:因为B(-1,m)在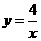 上, 所以
上, 所以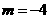
所以点B的坐标为(-1,-4) ···································································· 2分
又A、B两点在一次函数的图像上,
所以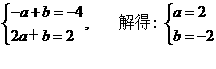 ·························································· 5分
·························································· 5分
所以所求的一次函数为y=2x-2 ······································· 6分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com