
题目列表(包括答案和解析)
13. 证明:(1)在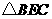 中,
中,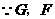 分别是
分别是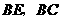 的中点
的中点
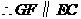 且
且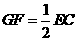
又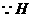 是
是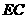 的中点,
的中点,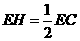 ,
,
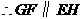 且
且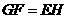
 四边形
四边形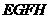 是平行四边形
是平行四边形
(2)证明: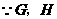 分别是
分别是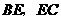 的中点
的中点
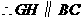 且
且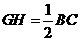
又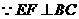 ,且
,且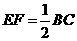 ,
,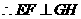 ,且
,且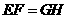
 平行四边形
平行四边形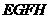 是正方形.
是正方形.
(2008山东德州)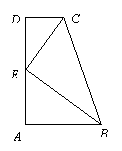 在梯形ABCD中,AB∥CD,∠A=90°, AB=2,BC=3,CD=1,E是AD中点.
在梯形ABCD中,AB∥CD,∠A=90°, AB=2,BC=3,CD=1,E是AD中点.
求证:CE⊥BE.
证明: 过点C作CF⊥AB,垂足为F.
∵ 在梯形ABCD中,AB∥CD,∠A=90°,
∴ ∠D=∠A=∠CFA=90°.
∴四边形AFCD是矩形.
AD=CF, BF=AB-AF=1.
在Rt△BCF中,
CF2=BC2-BF2=8,
∴ CF=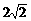 .
.
∴ AD=CF=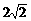 .
.
∵ E是AD中点,
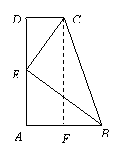 ∴ DE=AE=
∴ DE=AE=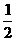 AD=
AD=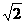 .
.
在Rt△ABE和 Rt△DEC中,
EB2=AE2+AB2=6,
EC2= DE2+CD2=3,
EB2+ EC2=9=BC2.
∴ ∠CEB=90°.
∴ EB⊥EC.
12. 解:当点M是AD的中点时,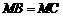 .
.
理由如下:如图,连结MB、MC,
∵在梯形ABCD中,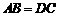 ,
,
∴梯形ABCD是等腰梯形,从而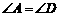 .
.
∵点M是AD的中点,∴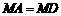 .
.
又∵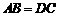 ,∴△MAB≌△MDC.
,∴△MAB≌△MDC.
∴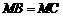 .
.
11. (1)(选证一)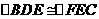
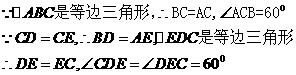
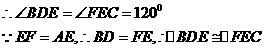
(选证二)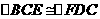
证明: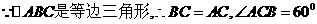

(选证三)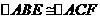
证明: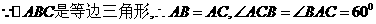

(2)四边形ABDF是平行四边形。
由(1)知,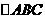 、
、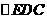 、
、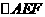 都是等边三角形。
都是等边三角形。
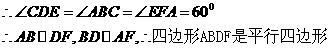
(3)由(2)知,)四边形ABDF是平行四边形。

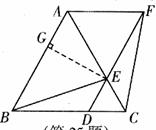
10. (1)证明: 与
与 都是等边三角形
都是等边三角形
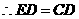
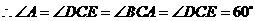 ················· 1分
················· 1分
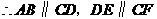 ······················· 2分
······················· 2分
又
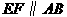

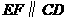 ···························· 3分
···························· 3分
 四边形
四边形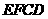 是菱形······················· 4分
是菱形······················· 4分
(2)解:连结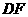 ,与
,与 相交于点
相交于点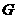 ················ 5分
················ 5分
由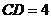 ,可知
,可知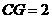 ······················ 6分
······················ 6分

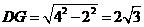 ······················· 7分
······················· 7分
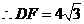 ···························· 8分
···························· 8分
9. ⑴ ①略;②PC-PA=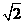 CE;⑵结论①仍成立;结论②不成立,此时②中三条线段的数量关系是PA-PC=
CE;⑵结论①仍成立;结论②不成立,此时②中三条线段的数量关系是PA-PC=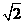 CE;
CE;
8. 解:(1) ∵△ABE、△BCF为等边三角形,
∴AB = BE = AE,BC = CF = FB,∠ABE = ∠CBF = 60°.
∴∠FBE = ∠CBA. ………………………1分
∴△FBE ≌△CBA.
∴EF = AC. ………………………………………2分
又∵△ADC为等边三角形,
∴CD = AD = AC.
∴EF = AD..……………………………………………………………………………………………………………3分
同理可得AE = DF. ……………………………………………………………………………………………5分
∴四边形AEFD是平行四边形. ……………………………………………………………………………6分
(其它证法,参照给分)
(2) 构成的图形有两类,一类是菱形,一类是线段.
当图形为菱形时,∠ BAC≠60°(或A与F不重合、△ABC不为正三角形)………7分
(若写出图形为平行四边形时,不给分)
当图形为线段时,∠BAC = 60°(或A与F重合、△ABC为正三角形). …………8分
7.
解:方案(1)
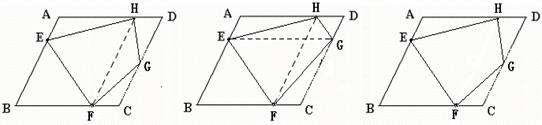
画法1: 画法2: 画法3:
(1)过F作FH∥AD交 (1)过F作FH∥AB交 (1)在AD上取一点
AD于点H AD于点H H,使DH=CF
(2)在DC上任取一点G (2)过E作EG∥AD交 (2)在CD上任取
连接EF、FG、GH、 DC于点G 一点G
HE,则四边形EFGH 连接EF、FG、GH、 连接EF、FG、GH、
就是所要画的四边形; HE,则四边形EFGH HE,则四边形EFGH
就是所要画的四边形 就是所要画的四边形
(画图正确得4分,简要说明画法得1分)
方案(2) 画法:(1)过M点作MP∥AB交AD于点P,
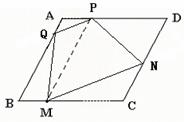 (2)在AB上取一点Q,连接PQ,
(2)在AB上取一点Q,连接PQ,
(3)过M作MN∥PQ交DC于点N,
连接QM、PN、MN
则四边形QMNP就是所要画的四边形
(画图正确的2分,简要说明画法得1分)
6. 答:四边形ABCD为菱形
理由是:
由翻折得△ABC≌△DBC.所以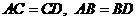
因为△ABC为等腰三角形,
所以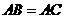
所以AC=CD=AB=BD,
故四边形ABCD为菱形
注:如果学生只答四边形ABCD为平行四边形给1分,说理正确,给5分,共6分
5. 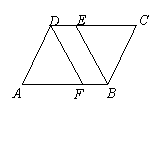 解:AF = CE
解:AF = CE
∵四边形ABCD是平行四边形
∴AD=CB, ∠A=∠C, ∠ADC=∠ABC
又∵∠ADF=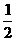 ∠ADC, ∠CBE=
∠ADC, ∠CBE=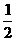 ∠ABC
∠ABC
∴∠ADF=∠CBE
∴∆ADF≌∆CBE
∴AF = CE
4.
猜想:
证明:
猜想: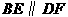 ,
,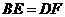
证明:
证法一:如图19-1
 四边形
四边形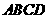 是平行四边形.
是平行四边形.
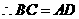
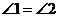
又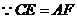
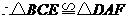
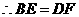
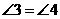
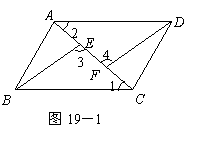
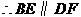
证法二:如图19-2
连结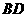 ,交
,交 于点
于点 ,连结
,连结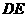 ,
,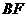 .
.
 四边形
四边形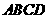 是平行四边形
是平行四边形
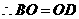 ,
,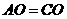
又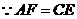
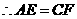
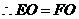
 四边形
四边形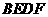 是平行四边形
是平行四边形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com