12．(2009年高考江西卷)△ABC中，A，B，C所对的边分别为a，b，c，tanC＝，sin(B－A)＝cosC.(1)求角A，C.(2)若S_△ABC＝3+，求a，c.

解：(1)因为tanC＝，即＝，

所以sinCcosA+sinCcosB＝cosCsinA+cosCsinB，

即sinCcosA－cosCsinA＝cosCsinB－sinCcosB，

得sin(C－A)＝sin(B－C)，

所以C－A＝B－C，或C－A＝π－(B－C)(不成立)，

即2C＝A+B，得C＝，所以B+A＝.

又因为sin(B－A)＝cosC＝，则B－A＝或B－A＝(舍去)，

得A＝，B＝.故A＝，C＝.

(2)S_△ABC＝acsinB＝ac＝3+，又＝，即 ＝，

得a＝2，c＝2.

11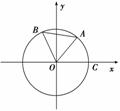．如图，点A，B是单位圆上的两点，A，B两点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，若点A的坐标为(，)，记∠COA＝α.

(1)求的值；(2)求|BC|²的值．

解：(1)∵A的坐标为(，)，根据三角函数的定义可知，sinα＝，cosα＝，∴＝＝.

(2)∵△AOB为正三角形，∴∠AOB＝60°.∴cos∠COB＝cos(α+60°)＝cosαcos60°－sinαsin60°.＝×－×＝，

∴|BC|²＝|OC|²+|OB|²－2|OC|·|OB|cos∠COB＝1+1－2×＝.

10．已知tanα＝2.求(1)tan(α+)的值；(2)的值．

解：(1)∵tan(α+)＝，tanα＝2，∴tan(α+)＝＝－3.

(2)＝＝＝tanα+＝.

9．(2010年江苏省南通市调研)已知＝1，tan(β－α)＝－，则tan(β－2α)＝________.

解析：因为＝1，即1－＝×，所以2tanα＝1，即tanα＝，所以tan(β－2α)＝tan(β－α－α)＝＝＝－1.

8．向量a＝(cos10°，sin10°)，b＝(cos70°，sin70°)，|a－2b|＝________________.

解析：|a－2b|²＝(cos10°－2cos70°)²+(sin10°－2sin70°)²＝5－4cos10°cos70°－4sin10°sin70°＝5－4cos60°＝3，∴|a－2b|＝.

7．(2010年无锡质检)的值为________．

解析：由已知得：原式＝＝＝.

6．若函数f(x)＝sin2x－2sin²x·sin2x(x∈R)，则f(x)的最小正周期为________．

解析：f(x)＝sin2x(1－2sin²x)＝sin2xcos2x＝sin4x，所以T＝＝.

5．若tanα+＝，α∈(，)，则sin(2α+)的值为_________．

解析：由题意知，tanα＝3，sin(2α+)＝(sin2α+cos2α)，而sin2α＝＝，cos2α＝＝－.∴sin(2α+)＝(－)＝－.

4.+2的化简结果是________．

解析：原式＝+2＝|2cos4|+2|sin4－cos4|＝－2sin4.

3．设a＝sin14°+cos14°，b＝sin16°+cos16°，c＝，则a、b、c的大小关系是

解析：a＝sin59°，c＝sin60°，b＝sin61°，∴a<c<b.

或a²＝1+sin28°<1+＝，b²＝1+sin32°>1+＝，c²＝，∴a<c<b.