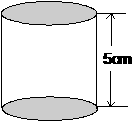
5.如图,假设圆柱的高是5cm,当圆柱的底面半径由小到大变化时,

　(1)圆柱的体积如何变化?　　　　　　　　　　　　　　 ,在这个变化过程中,自变量,因变量是什么?　　　　　　　　

(2)如果圆柱底面半径为r(cm),那么圆柱的体积V(cm3)可以表示为　　　　　　　　　　 .

(3)当r由1cm变化到10cm时,V由　　　　　　　 cm3变化到　　　　　　 cm3.

某校办工厂现在年产值是15万元，计划以后每年增加2万元.

写出年产值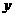(万元)与年数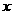之间的关系式.

用表格表示当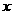从0变化到6(每次增加1)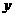的对应值.

求5年后的年产值.

3.

2.已知等腰三角形的底为3,腰长为x,则周长y可以表示为　　　　　 .

6、

一辆汽车以60千米/时的速度行驶，设行驶的路程为S(千米)，行驶的时间为

t(时)，则S与t的关系式是　　　　　　　

10、

甲乙两同学约定游戏规则:甲先骑自行车到终点后跑步回起点，而乙则跑步到终点后骑自行车回起点，两人同时出发，最后两人同时回到起点。已知甲骑自行车速度比乙骑自行车速度快，若某人离开起点的距离与所用时间的关系可用图象表示，则下列选项正确的是(　 　)

　　　　 (1)　　　　　　　　 (2)　　　　　　 (3)　　　　　　　　　 (4)

A、甲是图(1)，乙是图(2)；　　　　　　　 B、甲是图(3)，乙是图(2)；

C、甲是图(1)，乙是图(4)；　　　　　　 D 、甲是图(3)，乙是图(4)；

　 (2)若鱼塘中这种鱼的的总质量是(1)中估计的值，现在鱼塘中的鱼分大鱼和小鱼两类出售，大鱼每千克10元，小鱼每千克6元，要使小明家的此项收入不低于(1)中估计的收入，问：鱼塘中大鱼总质量应至少有多少千克？(5分)

下表是我国的几个省(自治区)的年降水量以及纬度位置。

表中的数字都是近似数，其中四个年降水量都是精确到100毫米得到的，那么广东省的年降水量1800毫米这个近似数有　　　　　　　　　　 个有效数字。

从表中可以看出，这四个省(自治区)年降水量随着纬度位置的变化而变化，这样请你说出在这个问题中，什么是自变量？什么是因变量？并说一说降水量是怎样随着纬度位置的变化而变化的？

某河受暴雨袭击，某天此河水的水位记录如下表：

上表反映的是哪两个变量之间的关系？

画折线图表示这两个变量之间的关系？

哪段时间内水位上升最快？

某下岗职工购进一批苹果，到集贸市场零售，已知卖出的苹果数x与y的关系如下表

写出用x表示y的关系式是＿＿＿＿＿。

一天，小军和爸爸去登山，已知山脚到山顶的路程为300米，小军先走了一段路程，爸爸才开始出发，图中两条线段分别表示小军和爸爸离开山脚登山的路程s(米)与登山所用的时间t(分钟)的关系(从爸爸开始登山时计时)。根据图象，下列说法错误的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 [　　 ]

A．爸爸开始登山时，小军已走了50米

B．爸爸走了5分钟，小军仍在爸爸的前面

C．小军比爸爸晚到山顶

D．爸爸前10分钟登山的速度比小军慢，10分钟之后登山的速度比小军快

　　 　　　　s(米)

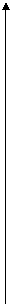
300

50

O　　　　　　 10　　　　　　　　　　　　 t(分钟)

在地球某地，温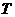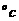度()与高度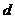()的关系可以近似

地用所示关系图来表示，当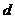的值分别是0，200，400，600时，

对应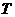的值分别为　　　　 　　　　　　　　　　　　　　。

9、

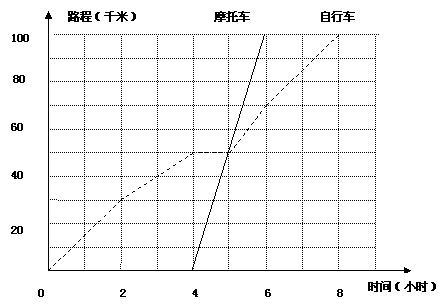　　 甲、乙两人(甲骑摩托车，乙骑自行车)从A城出发到100千米处的B城旅游，如图表示甲、乙两人离开A城路程与时间之间的关系图象。

分别求出甲、乙两人这次旅程的平均速度是多少？

根据图象，你能得出关于甲、乙两人旅行的那些信息？

注：回答2时注意以下要求：

(1)请至少提供三条相关信息，如由图象可知，乙比甲早出发4小时(或甲比乙晚出发4小时)等；(2)不要再提供(1)列举的信息。

小颖从家到学校是1000米，她以不变的速度从家出发20分钟到书店看了10分钟的书，接着她加快步伐匀速行走，用10分钟到了学校，下列图象中表示小颖从家到学校的时间(分)与路程(米)之间的关系是(　)

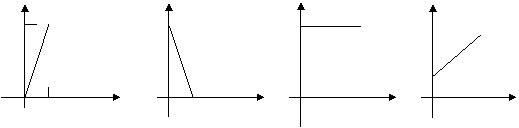
8、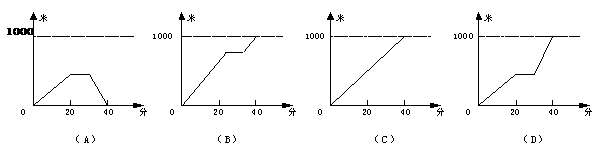一根蜡烛长20cm，点燃后每时燃烧5cm，燃烧时剩下的高度h与时间t(时)之间的关系图是()

A、 h　　　　　　　　 B、h　　　　 　　　C、 h　　　　　　　 D、h

　　　　 20　　　　　　　　　 20　　　　　　　　 20　　　　　　　　 20

　　　　　　 4　　　　 t　　　　　 4　　　 t　　　　　 4　　　 t　　　　　 4　 t　

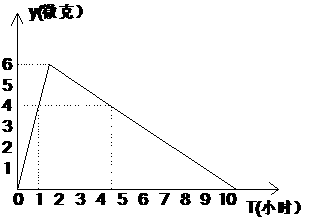
13、在全国抗击“非典”的斗争中，黄城研究所的医学专家们经过日夜奋战，终于研制出一种治疗非典的抗生药，据临床观察：如果成人按规定的剂量注射这种抗生素，注射药液后每毫升血液中的含药量y(微克)与时间t(小时)之间的关系近似地满足下图所示的折线．

(1)写出注射药液后自变量的取值范围．

(2)据临床观察：每毫升血液中含药量不少于4微克时，控制“非典”病情是有效的．如果病人按规定的剂量注射该药液后，那么这一次注射的药液经过多长时间后控制病情开始有效？这个有效时间有多长？

(3)假若某病人一天中第一次注射药液是早晨6点钟，问怎样安排此人从6:00-20:00注射药液的时间，才能使病人的治疗效果最好？

12、某种长途电话收费方式为按时收费,前3分钟收费1.8元,以后每加一分钟收费1元,求：

(1)当时间t3分钟时的电话费y (元)与t (分) 之间的关系.

(2)画出对应的”机器图”.

(3)计算当时间分别为5分、10分、30分、50分的电话费。

11、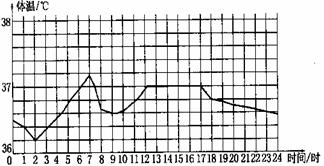小丽一天中的体温变化情况如图

(1)大约什么时候，小丽的体温最高？最高体温约是多少？

(2)大约什么时候，小丽的体温最低？最低体温约是多少？

(3)什么时间内，小丽的体温在升高？

(4)什么时间内，小丽的体温在降低？