
题目列表(包括答案和解析)
3.上午6点水箱里的温度是78℃,此后每小时下降4.5℃,求下午2点水箱内的温度.
解:下午2点即为14点
78-4.5×(14-6)=78-36=42(℃)
因此,下午2时水箱内的温度是42℃.
2.计算:
(1)(-125)×(-25)×(-5)×2×(-4)×8
(2)(-36)×(-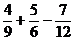 )
)
(3)(-56)×(-32)+(-44)×32
(4)-5×11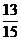
(5)4×(-96)×(-0.25)×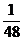
答案:(1)1000000;(2)7;(3)+384;(4)-59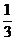 ;(5)2
;(5)2
1.下列各式变形各用了哪些运算律:
(1)12×25×(-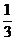 )×(-
)×(-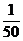 )=[12×(-
)=[12×(-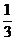 )]×[25×(-
)]×[25×(-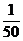 )]
)]
(2)(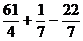 )×(-8)=
)×(-8)=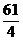 ×(-8)+(
×(-8)+(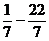 )×(-8)
)×(-8)
(3)25×[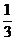 +(-5)+(+
+(-5)+(+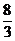 )]×(-
)]×(-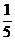 )=25×(-
)=25×(-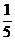 )×[(-5)+
)×[(-5)+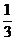 +
+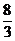 ]
]
答案:(1)乘法交换律和结合律
(2)加法结合律和乘法分配律
(3)乘法交换律和加法交换律
[例1]计算:
(1)(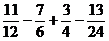 )×(-48)
)×(-48)
(2)1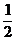 ×
×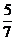 -(-
-(-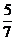 )×2
)×2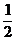 +(-
+(-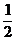 )×
)×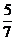
(3)49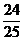 ×(-5)
×(-5)
分析:(1)小题根据题的特点,可直接利用乘法对加法的分配律.
(2)小题根据算式特点,逆用乘法对加法的分配律进行.
(3)小题直接计算较麻烦,根据其特点,可以把被乘数拆成两项,然后用分配律计算.
解:(1)原式=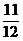 ×(-48)+(-
×(-48)+(-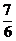 )×(-48)+
)×(-48)+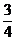 ×(-48)+(-
×(-48)+(-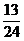 )×(-48)
)×(-48)
=-44+56+(-36)+26=2
(2)原式=1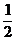 ×
×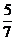 +
+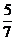 ×2
×2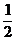 +(-
+(-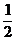 )×
)×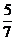
=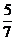 ×(1
×(1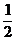 +2
+2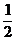 -
-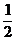 )
)
=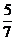 ×
×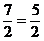
(3)原式=(50-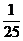 )×(-5)
)×(-5)
=50×(-5)-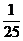 ×(-5)
×(-5)
=-250+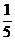 =-249
=-249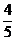 .
.
[例2]在某地区,夏季高山上的温度从山脚起每升高100米平均降低0.8 ℃,已知山脚的温度是24 ℃,山顶的温度是4 ℃,试求这座山的高度.
分析:这是一道与实际联系紧密的题,要弄清题意:已知山脚温度是24 ℃,山顶温度是4 ℃,这时可知山脚与山顶的温度差是20 ℃.题中又已知从山脚起每升高100米平均降低
0.8 ℃.要求这座山的高度,只需知道温度差里有多少个0.8,高度就有多少个100米,这样,本题即可解出.
解:根据题意,得这座山的高度为:
100×[(24-4)÷0.8]=100×25=2500(米)
2.ab=_______
∴3a+2b的值为_______,ab的值为_______.
*自我陶醉
编写一道自己感兴趣并与本节内容相关的题,解答出来.
测验评价结果:_______________;对自己想说的一句话是:_______________________.
求:1.3a+2b的值.
2.ab的值.
解:1.∵|a|=5,∴a=_______
∵|b|=2,∴b=_______
∵ab<0,∴当a=_______时,b=_______,
当a=_______时,b=_______.
∴3a+2b=_______或3a+2b=_______.
4.下列结论正确的是( )
A.-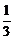 ×3=1 B.|-
×3=1 B.|-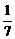 |×
|×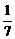 =-
=-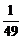
C.-1乘以一个数得到这个数的相反数 D.几个有理数相乘,同号得正
3.若m、n互为相反数,则( )
A.mn<0 B.mn>0
C.mn≤0 D.mn≥0
2.已知ab<|ab|,则有( )
A.ab<0 B.a<b<0
C.a>0,b<0 D.a<0<b
1.若mn>0,则m,n( )
A.都为正 B.都为负
C.同号 D.异号
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com