
题目列表(包括答案和解析)
2. 探索
探索
在图1至图3中,已知△ABC的面积为a .
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连结
DA.若△ACD的面积为S1,则S1=______(用含a的代数式
 表示);
表示);
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,
使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则
S2=__________(用含a的代数式表示);
 (3)在图2的基础上延长AB到点F,使BF=AB,连结FD,
(3)在图2的基础上延长AB到点F,使BF=AB,连结FD,
FE,得到△DEF(如图3).若阴影部分的面积为S3,则
S3=__________(用含a的代数式表示),并运用上述(2)的
结论写出理由.
发现
像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的 倍.
应用
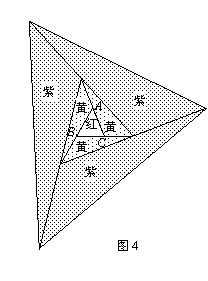 要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种黄花,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:
要在一块足够大的空地上栽种花卉,工程人员进行了如下的图案设计:首先在△ABC的空地上种红花,然后将△ABC向外扩展三次(图4已给出了前两次扩展的图案).在第一次扩展区域内种黄花,第二次扩展区域内种紫花,第三次扩展区域内种蓝花.如果种红花的区域(即△ABC)的面积是10平方米,请你运用上述结论求出:
(1)种紫花的区域的面积;
(2)种蓝花的区域的面积.
两条平行直线上各有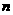 个点,用这
个点,用这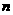 对点按如下的规则连接线段;
对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当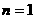 时的情况,此时图中三角形的个数为0;
时的情况,此时图中三角形的个数为0;
图2展示了当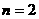 时的一种情况,此时图中三角形的个数为2;
时的一种情况,此时图中三角形的个数为2;
(1)当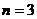 时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当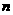 对点时,按上述规则画出的图形中,最少有多少个三角形?
对点时,按上述规则画出的图形中,最少有多少个三角形?
 (3)当
(3)当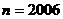 时,按上述规则画出的图形中,最少有多少个三角形?
时,按上述规则画出的图形中,最少有多少个三角形?
图(1) 图(2) 图(3)
提升能力 挑战自我
1.如图,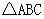 中,延长
中,延长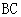 到
到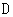 ,
,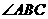 和
和 的平分线相交于点
的平分线相交于点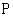 ,爱动脑筋的晓敏同学在写作业时,发现如下规律:
,爱动脑筋的晓敏同学在写作业时,发现如下规律:
(1) 若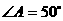 ,则
,则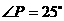 ;
;
(2) 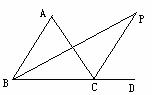 若
若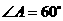 ,则
,则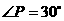 ;
;
(3) 若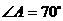 ,则
,则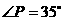 ;
;
(4)
根据上述规律,若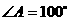 ,则
,则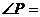 ______.
______.
(5)
请你用数学表达式归纳出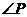 与
与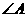 的关系:______.
的关系:______.
(6) 请你证说明你的结论.
5.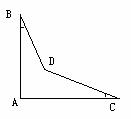 一个零件的形状如图,按规定
一个零件的形状如图,按规定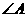 应等于
应等于 ,
,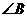 和
和 应分别
应分别
是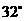 和
和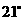 .检验工人量得
.检验工人量得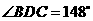 ,就断定这个零件不
,就断定这个零件不
合格.运用三角形的有关知识说明零件不合格的理由.
4.已知等腰三角形一腰上的中线将三角形的周长分成 和
和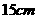 两部分,求这个三角形腰长和底边的长.
两部分,求这个三角形腰长和底边的长.
3.如图,△ABC中,∠B=32°,∠C=55°,AD⊥BC于D,
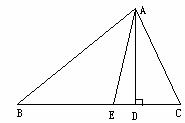 AE平分∠BAC交BC于E,求∠EAD的度数.
AE平分∠BAC交BC于E,求∠EAD的度数.
2.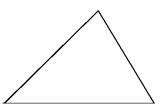 如图所示是一块三角形优质土地,现引进良种进行对比试验,需将这块土地分成面积相等的四块,请你设计分法方案.
如图所示是一块三角形优质土地,现引进良种进行对比试验,需将这块土地分成面积相等的四块,请你设计分法方案.
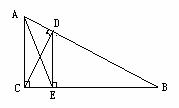
1.如图,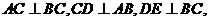 垂足分别为
垂足分别为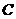 、
、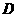 、
、 .现有下列说法:
.现有下列说法:
(1)
在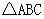 中,
中,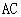 是
是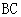 边上的高;
边上的高;
(2)
 在
在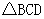 中,
中,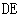 是
是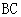 边上的高;
边上的高;
(3)
在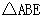 中,
中,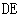 是
是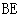 边上的高;
边上的高;
(4)
在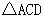 中,
中,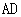 是
是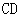 边上的高.
边上的高.
其中,哪些是正确的?哪些是不正确的?
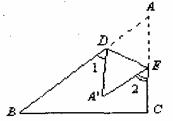
8.如图,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A的大小等于____________度.
7.用7根火柴棒首尾顺次连接摆成一个三角形,能摆成不同的三角形的个数为 .
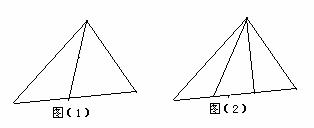
6.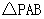 的
的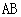 边上任取一点
边上任取一点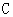 (异于
(异于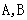 ),连结
),连结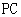 ,可以得到3个不同的三角形(如图(1));在
,可以得到3个不同的三角形(如图(1));在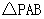 的
的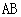 边上任取两点
边上任取两点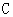 、
、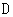 (异于
(异于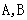 ),分别连结
),分别连结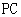 、
、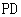 ,可以得到
,可以得到
个不同的三角形(如图(2));要得到15个不同的三角形,可以在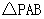 的
的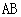 边上任取
个点(异于
边上任取
个点(异于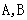 ),分别与点
),分别与点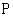 连结即可.
连结即可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com