
题目列表(包括答案和解析)
6. 多项式2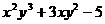 是 次 项式.
是 次 项式.
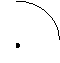
5. 在平地上投掷手榴弹,下面哪幅图可以大致刻画出手榴弹投掷过程中(落地前)速度变化情况( )

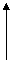
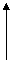
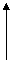
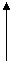 v
v
v
v
v
v
v
v
 |
 |
||||||||
|
|||||||||
|
|||||||||
|
|||||||||



 A
B C
D
A
B C
D
第二卷(非选择题)
4. 如图,ΔABC,AB = AC, AD⊥BC, 垂足为

 D, E是AD上任一点,则有全等三角形( )
•E
D, E是AD上任一点,则有全等三角形( )
•E
A. 1对; B. 2对; C. 3对; D. 4对. B D C
3. 1纳米等于( )
A. 1×10-6米; B. 1×106米;

 C. 1×10-9米;
D. 1×109立方米. A
C. 1×10-9米;
D. 1×109立方米. A
2.下面计算错误的是( )
A.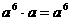 ;B.
;B.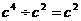 ;C.
;C.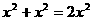 ;D.
;D.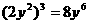 .
.
1.一正方体的棱长为2×103毫米, 则其体积可表示为( )立方米.
A.8×109; B. 8×100; C. 2×1027; D. 6×109.
(1) 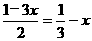
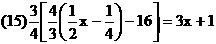
3)解方程组: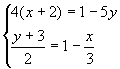 4)已知
4)已知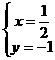 是方程组
是方程组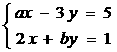
的一个解,求3(a-b)-a2的值
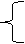 四 已知方程组 3kx+2y=6k 的解满足方程x+y=10, 求k(5分)
四 已知方程组 3kx+2y=6k 的解满足方程x+y=10, 求k(5分)
2x+y=8
五 小明家的鱼塘养了某种鱼2000条,现准备打捞出售,为了估计鱼塘中的这种鱼的总质量,现从鱼塘中捕捞了3次,得到数据如下:
|
|
鱼的条数 |
平均每条鱼的质量 |
|
第一次捕捞 |
15 |
1.6千克 |
|
第二次捕捞 |
15 |
2.0千克 |
|
第三次捕捞 |
10 |
1.8千克 |
(1)鱼塘中这种鱼平均每条质量约是 千克,鱼塘中所有这种鱼的总质量约是 千克;若将这些鱼不分大小,按每千克7.5元的价格出售,小明家约可收入 元;
(2)若鱼塘中这种鱼的的总质量是(1)中估计的值,现在鱼塘中的鱼分大鱼和小鱼两类出售,大鱼每千克10元,小鱼每千克6元,要使小明家的此项收入不低于(1)中估计的收入,问:鱼塘中大鱼总质量应至少有多少千克?(5分)
六 已知: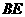 平分
平分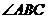 ,
,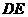 ∥
∥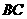 ,
,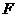 为
为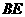 中点,试说明:
中点,试说明: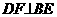 。(4分)
。(4分)
四 列方程(组)应用题
1) 某工人原计划用26天生产一批零件,工作了2天后,因改变了操作方法,每天比原来多生产5个零件,结果提前了4天完成了任务,问原来每天生产多少个零件,这批零件共有多少个?(4分)
2)有一个只允许单向通过的窄道口,通常情况下,每分钟可以通过9人。一天,王老师过道口时发现由于道口拥挤每分钟只能通过3人,而他前面还有36 人等待通过(假设先到的先过,王老师过道口的时间忽略不计),通过道口后,还需7分钟到达学校。
(1) 此时,若绕道口而行,要15分钟到达学校,从节省时间考虑,王老师应选择绕道去学
校,还是选择通过拥挤的道口去学校?
在王 (2)若在王老师等人的维持下,几分钟后,秩序恢复正常(维持秩序期间,每分钟仍有3人通过道口),结果王老师比拥挤的情况下提前了6分钟通过道口,问维持的时间是多少?(6分)
1、如图,DE⊥AB,DF⊥AC,AE=AF,找出一对全等三角形,并说明理由。
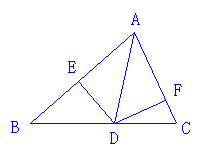
图为一位旅行者在早晨8时从城市出发到郊外所走的
路程与时间的变化图。根据图回答问题。
(1) 9时,10时30分,12时所走的路程分别是多少?
答:
(2)  他休息了多长时间?
他休息了多长时间?
答:
(3) 他从休息后直至到达目的地这段时间的平
均速度是多少?
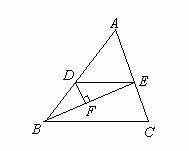
已知:如图BC∥EF,BC=EF,AB=DE;
说明AC与EF相等。
解:∵BC∥EF(已知)
∴∠ABC=∠__________( )
在△ABC和△DEF中
 ______=_______
______=_______
∵ _______=________
______=________
∴△ABC≌___________ ( )
∴ _______=__________ ( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com