7，一件工作，小张单独做6天完成，小李单独做需12天完成，若他们合做需___天可以完成.

8，甲乙两人比赛登楼梯，他俩从36屋的长江大厦底层出发,当甲到达6楼时，乙刚好到达5楼，按此速度，当甲到达顶层时，乙可到达______层.

9，含盐5%的盐水40千克，其中含水是__________千克.

10，三角形的周长是84cm，三边长的比为17∶13∶12，则这个三角形最短的一边长为　　 .

11，一块长、宽、高分别为4cm，3cm，2cm的长方体橡皮泥，要用它来捏一个底面半径为1.5cm的圆柱，若它的高为xcm，则可列方程　　 ____.

12，某月有五个星期日，已知这五个日期的和为75，则这月中最后一个星期日是　　 号.

13，连续的三个奇数的和为33，则这三个数为　　　 .

14，一件服装进价200元，按标价的8折销售，仍可获利10%，该服装的标价是＿＿＿元.

1，一种小麦的出粉率是80%，那么200千克这种小麦可出粉(　　 )

A.80千克　　　　　　　 B.160千克　　　　　　 C.200千克　　　　　　 D.100千克

2，小新比小颖多5本书，小新是小颖的2倍，小新有书(　　 )

A.10本　　　　　 B.12本　 　　C.8本 　　D.7本

3，父子年龄和是60岁，且父亲年龄是儿子的4倍，那么儿子(　　 )

A.15岁　　　　　 B.12岁　　　　　　　　 C.10岁　　　　　　　　 D.14岁

4，内径为120mm的圆柱形玻璃杯，和内径为300mm，内高为32mm的圆柱形玻璃盆可以盛同样多的水，则玻璃杯的内高为( 　 )

A.150mm　 　　 B.200mm　 　　 C.250mm　　 　 D.300mm

5，父子二人早上去公园晨练，父亲从家出了跑步到公园需30分钟，儿子只需20分钟，如果父亲比儿子早出发5分钟，儿子追上父亲需(　)

A.8分钟　　　 　　B.9分钟　　　　　 C.10分钟　 　　　　D.11分钟

6，一个两位数的十位上的数字与个位上数字之和为8，把这个数减去36后，结果恰好成为十位数字与个位数字对调后组成的两位数，则这个两位数是(　)

　　 A.26　　　　　 B.62　　　　　 C.71　　　　 D.53

22．已知x=5-t，y-3=2t，则x与y之间的关系式是_______．

[探究学习]苏步青巧解数学趣题的启示

　　 我国著名数学家苏步青在访问德国时，德国一位数学家给他出了这样一道题目：

　　 甲、乙二人相对而行，他们相距10千米，甲每小时走3千米，乙每小时走2千米，甲带着一条狗，狗每小时跑5千米，狗跑得快，它同甲一起出发，碰到乙的时候向甲跑去，碰到甲的时候又向乙跑去，问当甲、乙两人相遇时，这条狗一共跑了多少千米？

　　 苏步青教授很快就解出了这道题目．同学们，你知道他是怎么解的吗？

　　 这道题最让人迷惑不解的是甲身边的那条狗．如果我们先计算狗从甲的身边跑到乙的身边的路程s，再计算狗从乙的身边跑到甲的身边的路程s，……，显然把狗跑的路程相加，这样很繁琐，笨拙且不易计算．苏教授从整体着眼，根据甲、乙出发到相遇经历的时间与狗所走的时间相等，即10÷(3+2)=2(小时)，这样就不难求出狗一共跑的路程是：5×2=10(千米)．

　　 苏步青教授在解题时，把注意力和着眼点放在问题的整体结构上，从而能触及问题的实质：狗从出发到甲、乙两相遇所用的时间，恰好是甲、乙二人相遇所用的时间，从而使问题得到巧妙的解决．苏教授这种解决问题的思想方法实际上就是数学中的整体思想的应用．对于某些数学问题，灵活运用整体思想，常可化难为易，捷足先登．在解二元一次方程组时，也要注意这种思想方法的应用．

　　 比如解方程组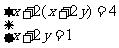

　　 解：把②代入①得x+2×1=4，所以x=2

　　 把x=2代入②得2+2y=1，解之，得y=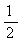

　　 所以方程组的解为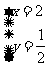

　　 同学们，你会用同样的方法解下面两个方程吗？试试看!

　　 (1)

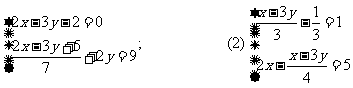
21．已知二元一次方程组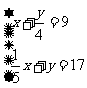的解为x=a，y=b，则│a-b│=(　 )

　　 A．1　　 B．11　　 C．13　　 D．16

20．请思考：方程组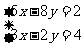的解是不是方程8x-10y=6的一个解．

19．若│x+y-2│+(x-y)²=0，那么x=________，y=________．

18．已知的解，求a、b的值．

17．在y=kx+b中，当x=1时，y=2；当x=2时，y=4，那么k=_______，b=_______．

16．用代入法解下列方程组：

(1)　　　　　　　　　

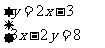
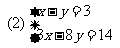
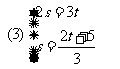
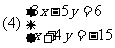
[综合创新训练]

15．若x-3y=2x+y-15=1，则x=______，y=_______．