
题目列表(包括答案和解析)
2. 正数大于零,零大于负数,正数大于一切负数,两个负数比较,绝对值大的反而小。
(6) 实数中的非负数及其性质
在实数范围内,正数和零统称为非负数
我们已经学过的非负数有如下三种形式
(9) ⑴任何一个实数a的绝对值是非负数,即 ≥0
≥0
(10) ⑵任何一个实数的平方是非负数,即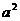 ≥0;
≥0;
(11) ⑶任何一个非负数a的算术平方根是非负数,即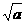 ≥0
≥0
(12) 非负数有以下性质
(13) ⑴非负数有最小值零
(14) ⑵有限个非负数之和仍然是非负数
(15) ⑶几个非负数之和等于0,则每个非负数都等于0。
(16) 11..二次根式的两条运算法则
(17) 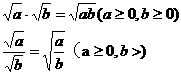
(
实数练习题二
1. 在数轴上表示的两个数,右边的数总比左边的数大。
10.实数
(1) 概念:________和________统称为实数。
(2)  分类 按定义
分类 按定义
 _______
_______
 ________
________
 _______
_______
________ ___ 有限小数或________小数
 _______
_______
实数 ________
_______
 _________
_________
________ 无限不循环小数
_________
 按大小 正实数
按大小 正实数
实数 零
负实数
(4) (3)实数的有关性质
(5) ⑴a与b互为相反数〈=〉a+b=0
(6) ⑵a与b互为倒数〈=〉ab=1
(7) ⑶任何实数的绝对值都是非负数,即 ≥0
≥0
(8) ⑷互为相反数的两个数的绝对值相等, 即 =
=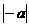
⑸正数的倒数是正数;负数的倒数是负数;零没有倒数.
(4)实数和数轴上的点的对应关系:
实数和数轴上的点是一一对应的关系
(5) 实数的大小比较
9.立方根
(1) 定义:______________________________.
(2) 数a的立方根的表示方法:_________
(3) 互为相反数的两个数的立方根之间的关:_________
(4)
两个重要的公式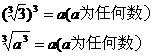
8.a2的算术平方根的性质
①当a≥0时,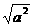 =( ) ② 当a<0时,
=( ) ② 当a<0时,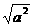 =( )
=( )
一般的,当a<0时,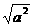 =-a.
=-a.
我们还知道,当a≥0时,│a│=a;当a<0时,│a│=a.
综上所述,有
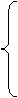 a (a≥0)
a (a≥0)
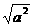 =│a│=
=│a│=
-a (a<0)
从算术平方根的定义可得: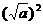 =a (a≥0)
=a (a≥0)
7.开方运算:
(1) 定义:
① 开平方运算:
② 开立方运算:
(2)平方与开平方式( )关系,故在运算结果中可以相互检验。
6.平方根与算术平方根的区别与联系:
区别:①定义不同 ②个数不同:
③ 表示方法不同:
联系:①具有包含关系:
②存在条件相同:
③ 0的平方根和算术平方根都是0。
5.平方根
(1) 定义:
(2) 非负数a的平方根的表示方法:
(3) 性质: 一个( )有两个平方根,这两个平方根( )。
( )只有一个平方根,它是( )。
( )没有平方根。
说明:平方根有三种表示形式:±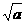 ,
,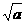 ,-
,-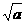 ,它们的意义分别是
,它们的意义分别是
:非负数a的平方根,非负数a的算术平方根,非负数a的负平方根。要特别注意: 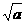 ≠±
≠±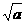 。
。
4.算术平方根。
(1) 定义:
(2) 我们规定:
(3)
性质:算术平方根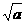 具有双重非负性:
具有双重非负性:
① 被开方数a是非负数,即a≥0.
②
算术平方根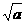 本身是非负数,即
本身是非负数,即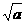 ≥0。
≥0。
也就是说,( )的算术平方根是一个正数,
0的算术平方根是( ),
( )没有算术平方根。
3.常见的无理数类型
(1) 一般的无限不循环小数,如:1.41421356¨···
(2) 看似循环而实际不循环的小数,如0.1010010001···(相邻两个1之间0的个数逐次加1)。
(3) 有特定意义的数,如:π=3.14159265···
(4).开方开不尽的数。如: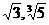 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com