2．已知关于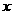的方程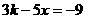的解是非负数，则 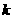的取值范围为　　　　　 ．

1．不等式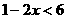的负整数解是 　　　　　　　　　　　　．

(八)板书设计(题目用投影)

勾股定理的内容 　　　　例1 　　分析过程　　　　　　　　　 练习板演

直角三角形两直角边的平方和

等于斜边的平方)

几何语言:

∵Rt△ABC中，∠C＝ 90°

∴

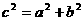
(七)布置作业：

课本P106习题2、3、4 ; P108 B组4。

(六)课堂小结：

主要通过学生回忆本节课所学内容，从内容、应用、数学思想方法、获取新知的途径方面先进行小结，后由教师总结。

(四)、问题解决：

让学生解决开头的实际问题，前后呼应，学生从中能体会到成功的喜悦。完成课本“想一想”进一步体会勾股定理在实际生活中的应用，数学是与实际生活紧密相连的。

(五)、练习

　 1、Rt△ABC中，∠C＝ 90°

(1)a=6，b=10。求b

(2)c=25，b=15。求a

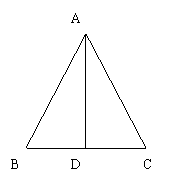
2、如图、　 等边△ABC的边长是6㎝

(1)求高AD的长

(2)求S_△ABC

(二)、勾股定理的探索，证明过程及命名

1、实验操作(探索-猜想)：

教师用计算机演示(利用几何画板)：

　　 (1)在△ABC中，∠A，∠B，∠C所对边分别为a，b和 c， ∠ACB＝ 90°，使△ABC运动起来，但始终保持∠ACB＝90°，如拖动 A点或B点改变a ,b的长度来拖动AB边绕任一点旋转△ACB等．

(2)在以上过程中，始终测算a²，b²，c²，各取以上典型运动的某一两个状态的测算值(约3-5个)列成表格，让学生观察三个数之间有何数量关系，得出猜想．

　(直角三角形两直角边的 平方和等于斜边的平方)

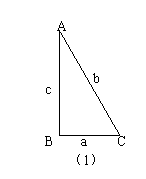(3)引导学生用符号语言表示，因为将文字语言转化为数学语言是学习数学学习的一项基本能. 接着教师向学生介绍“勾，股，弦”的含义.

∵Rt△ABC中，∠C＝ 90°

∴AB²=AC²+BC²(或)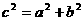

2．证明猜想．

目前世界上可以查到的证明勾股定理的方法有几百种，连美国第20届总统加菲尔德于1881年也提供了面积证法(见课本第107页图(4))，而我国古代数学家利用割补、拼接图形计算面积的思路提供了很多种证明方法，下面咱们采纳其中一种(教师制作教具演示，见如图4－18)来进行证明．(分析引导让学生写出证明步骤)

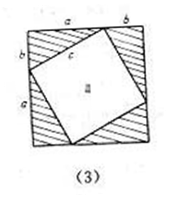拼成一个大正方形(边长为a+b)则:

4×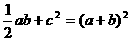

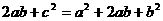
整理，得: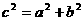　　　　　　　　　　　　　　　　　　　　

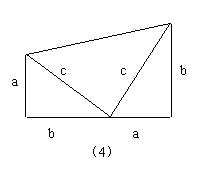根据梯形的面积公式可得:

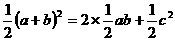
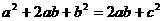
整理，得: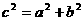

3．勾股定理的命名．

　我国称这个结论为“勾股定理”，西方称它为“毕达哥拉斯定理”，为什么呢？

　　 (1)介绍《周髀算经》中西周的商高(公元一千多年前)发现了勾三股四弦五 这个规律

　　 (2)介绍西方毕达哥拉斯于公元前582-493时期发现了勾股定理；

(3)康熙数学专著《勾股图解》有五种求解直角三角形的方法,积求勾股法是其独创；

　　 (4)对比以上事实对学生进行爱国主义教育，激励他们奋发向上．

4、归纳勾股定理的几何语言:

∵Rt△ABC中，∠C＝ 90°∴AB²=AC²+BC²(或、、)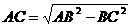

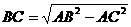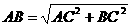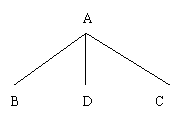(三)、勾股定理的应用

　　 　已知直角三角形任两边求第三边．

例 1　 在△ABC中， AB=AC=10㎝，

BC=16㎝,高为AD

(1)求AD的长；(2)求△ABC的面积

(一)提出问题：

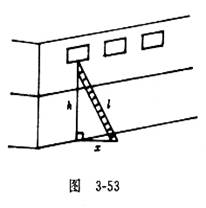首先创设这样一个问题情境：某楼房三楼失火，消防队员赶来救火，了解到每层楼高h=3米，消防队员取来6.5米长的云梯,如果梯子的底部离墙基的距离x=2.5米,请问消防队员能否进入三楼灭火?问题设计具有一定的挑战性,目的是激发学生的探究欲望,教师引导学生将实际问题转化成数学问题,也就是“已知一直角三角形的两边，如何求第三边？” 的问题。学生会感到困难，从而教师指出学习了今天这一课后就有办法解决了。这种以实际问题为切入点引入新课，不仅自然，而且反映了数学来源于实际生活，数学是从人的需要中产生这一认识的基本观点，同时也体现了知识的发生过程，而且解决问题的过程也是一个“数学化”的过程。

本课的教学难点：用面积法(拼图法)证明勾股定理。

4、 通过介绍勾股定理在中国古代的研究，激发学生热爱祖国，热爱祖国悠久文化的思想，激励学生发奋学习。