
题目列表(包括答案和解析)
6、一元二次方程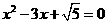 的根的情况是( )
的根的情况是( )
A、有两个不相等的实数根 B、有两个相等的实根
C、没有实数根 D、不能确定
5、若方程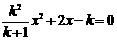 是关于x的一元二次方程,则k的取值范围是( )
是关于x的一元二次方程,则k的取值范围是( )
A、 k≠0 B、k≠-1 C、k≠0且k≠-1 D、k〉0或k〈-1
4、已知关于x的方程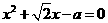 的一个根是1
的一个根是1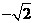 ,则a的值为( )
,则a的值为( )
A、1 B、-1 C、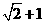 D、1
D、1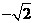
3、若关于x的一元二次方程kx2+2x+1=0有实数根,则k的取值范围是( )
A、k〈1 B、k≤1 C、k= 1 D、k≤1且k≠0
2、
 方程
方程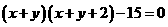 把
把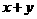 看作未知数时,
看作未知数时,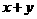 的值为( )
的值为( )
A、-5或3 B、-3或5 C、3 D、5
1、在下列方程中,一定是关于x的一元二次方程的是( )
A、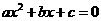 B、
B、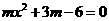
C、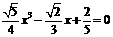 D、
D、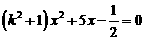
24.(本题14分)
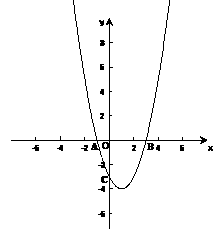
如图,在直角坐标平面中,O为坐标原点,二次函数y=ax2+bx+c的图象与x轴相交于点A、B,与y轴交于点C,点A的坐标是(-1,0)点C的坐标为(0,-3),且BO=CO
(1) 求出B点坐标和这个二次函数的解析式;(5分)
(2) 求△ABC的面积。(4分)
(3) 设这个二次函数的图象的顶点为M,求AM的长.(5分)
23.(本题12分) 已知,正比例函数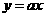 图象上的点的横坐标与纵坐标互为相反数,反比例函数
图象上的点的横坐标与纵坐标互为相反数,反比例函数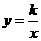 在每一象限内y随x的增大而减小,一次函数y=k2x-2a+4的图象经过点
在每一象限内y随x的增大而减小,一次函数y=k2x-2a+4的图象经过点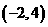 .
.
(1)求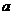 的值.(5分)
的值.(5分)
(2)求一次函数和反比例函数的解析式.(7分)
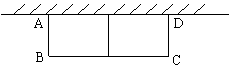
22.(本题lO分) 如图,有长为24米的篱笆,一面利用墙(图中的阴影阴影部分就是墙,墙的最大可利用长度为10米),围成中间隔有一道篱笆的长方形花圃.花圃的宽AB为x米,面积为S米2.
(1)求S与x的函数关系式;
(2)当x为多少时,围成的花圃面积最大?最大面积是多少?
20.(本题8分) 某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么半月内可售出口400件,根据销售经验,提高单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件。如何提高售价,才能在半月内获得最大利润?
2l(本题10分) 如图,一次函数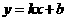 的图象与反比例函数
的图象与反比例函数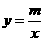 的图象相交于A、B两点,(1)利用图中条件,求反比例函数和一次函数的解析式(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
的图象相交于A、B两点,(1)利用图中条件,求反比例函数和一次函数的解析式(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com