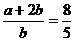6、　 若，则=_______________.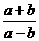

5、　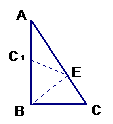 蜗牛前进的速度只有某人步行速度的1000分之一，若此人步行的速度是每小时5.4公里，则蜗牛爬行的速度是每秒　　　　　 公里。

4、　 一颗正方体骰子，六个面上的数字分别为1、2、3、3、4、5，投掷一次，向上的面出现数字为3的概率为_____________

3、　 当k = _________时，方程kx²+2x-1=0有两个不相等的实数根。

2、　 方程x² = -x的解为_________；当x=　　　　 ，函数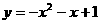的值为0。

1、　 计算：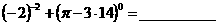　

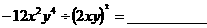
当x=_______时， 代数式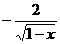有意义；函数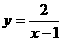的自变量取值范围

31、(本题满分10分)已知：等边△ABC和点P，设点P到△ABC三边AB、AC、BC的距离分别为h₁、h₂、h₃，△ABC的高为h。若点P在一边BC上(如图7)，此时h₃=0，可得结论：h₁+h₂+h₃=h。请直接应用上述信息解决下列问题：当点P在△ABC内(如图8)、点P在△ABC外(如图9)这两种情况时，上述结论是否成立？若成立，请给予证明；若不成立，h₁、h₂、h₃与h之间又有怎样的关系，请写出你的猜想，不需要证明。

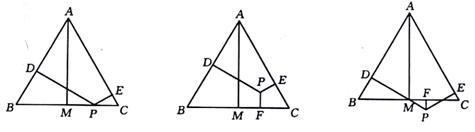
　　　　　　　 图7　　　　　　　　　 图8　　　　　　　　　　 图9

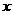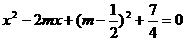30、(本题满分8分)已知：四边形ABCD中，AB∥CD，且AB、CD的长是关于的方程的两个根。

　 (1)当m=2或m>2时，四边形ABCD分别是哪种四边形？请说明理由。

　 (2)若M、N分别是AD、BC的中点，线段MN分别交AC、BD于点P、Q，PQ=1且AB<CD，求AB、CD的长。

(3)在(2)的条件下，AD=BC=2，求一个一元二次方程，使它的两个根分别是tan∠BDC和tan∠BCD。

29、(本题满分9分)如图5，⊙O的直径为AB，过半径OA的中点G作弦CE⊥AB，在弧AB上取一点D，分别作直线CD、ED，交直线AB于点F、M。

(1)求∠COA和∠FDM的度数；

(2)求证：△FDM∽△COM；

(3)如图6，若将垂足G改取为半径OB上任意一点，点D改取在弧EB上，仍作直线CD、ED，分别交直线AD于点F、M。试判断：此时是否仍有△FDM∽△COM？证明你的结论。

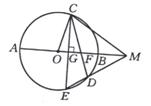
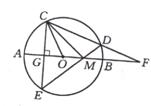
图5　　　　　　　　　　　 图6

28、(本题满分8分)某校的校门是一抛物线形水泥建筑物，如图所示，大门的地面宽度为8m，两侧距地面4m处各有一个挂校名横匾用的铁环，两铁环的水平距离为6m。

(1)求校门的高为多少米(水泥建筑物的厚度不计)？

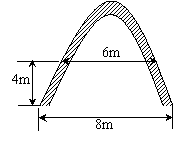(2)由于学校正在改善办学条件，有一高5m、宽5m的大型工程车需进入校园，问该车能否顺利从校门通过？