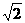29、(10′)如图，已知在△ABC中，AC=14,BC=6,∠ACB=45°,点O在AC上移动，⊙O始终和AB相切，切点为D，⊙O与AC交于E、F两点，(点F可在AC的延长线上)(1)设⊙O的半径为r，在满足题意的点O中，是否存在某一位置，使得⊙O与AB、BF都相切，若不存在，请说明理由；若存在，求出此时r的长　 (2)设四边BDOC形的面积为S，求S与r的函数关系式及r的取值范围.

28、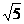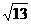(8′)⑴如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点

①在图1中以格点为顶点画一个三角形，使三角形三边长分别为2、　 、、

②在图2中以格点为顶点画一个面积为10的正方形

③观察图3中阴影部分，请你将它适当剪开，重新拼成一个面积不变的正方形(要求：在图中用虚线作出，并用文字说明)

④观察正方体图形，沿着一些棱将它剪开，展成平面图形，若正方体的表面积为12，请在图4中以格点为顶点画一个正方体的平面展开图。(只需画出一种图形)

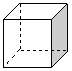
　　 图1　　　　　 图2　　　　　　 图3

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图4

(3′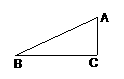)⑵如图，已知△ABC，∠C＝90°，试用尺规作一个等腰△ABD，

使点D在直线BC或直线AC上．(只需作一个，不写作法，保留

作图痕迹)；②这样的等腰三角形有　　 个．

27、某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元，设矩形的一边长为x米，面积为s平方米

(1)求出s与x之间的函数关系式，并确定自变量x的取值范围

(2)请你设计一个方案，使获得的设计费最多，并求出这个费用

※(3)为使广告牌美观、大方，要求做成黄金矩形，请你按要求设计，并计算出可获得的设计费是多少？(精确到元)

(参考资料：①当矩形的长是宽与(长+宽)的比例中项时，这样的矩形叫黄金矩形；②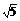≈2.236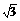，≈1.732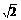，≈1.414)　 (9′)

26、如图，Rt△ABE中，∠B＝90°，以AB为直径的⊙O交斜边于C，CE的垂直平分线FD交BE于D，连结BD．⑴试判断CD与⊙O的位置关系，并加以证明；⑵若AC·AE＝12，求⊙O的半径．(8′)

25、如右表，表中所给的每行三个数a、b、c有a<b<c，根

据表中已有的数的规律，试写出当a=20时，b、c的值，并

把b、c用a的代数式表示出来. (6′)

24、如图(1)，A、E、F、C在同一条直线上，AE=CF，过E、F分别作DE⊥AC，BF⊥AC，若AB=CD，①求证：BD平分EF.　 ②若将△DEC的边EC沿AC方向移动变为图(2)时，其余条件不变，试判断上述结论是否成立，并说明理由. (8′)

23、如图，⊙O的直径AB与弦CD垂直，F为CD延长线上一点，连AF交⊙O于E点，

求证：AC²=AE·AF　 (6′)

21、计算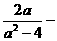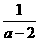：⑴ 　　　　　⑵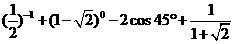 　　

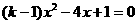(3)解方程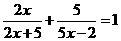：　　　 22、已知关于x的方程

有实根，求k的取值范围　 (6′)

20、如图：这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后，在地面上形成阴影(圆形)的示意图，已知桌面的直径为1.2米，桌面距离地面1米，若灯泡距离地面3米，则地面上阴影部分的面积为　 (　 　　)　　　　　　　　　　　　　　　　　　　　　

A.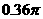平方米　 　　B.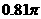平方米　　 C.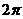平方米 　　D.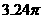平方米

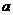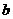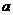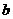19、如图分别按A、B两种方法用钢丝绳捆扎圆形钢管的截面图：设A、B两种方法捆扎所需的绳子的长分别为、，则、的大小关系为　　　　　　　　　　　 (　　 )

A．等于　　　　 B.小于　　　　　 C.大于　　　　　　 D.无法确定