6、命题“有三个角对应相等的两个三角形全等”，它的题设是　　　 　　　　　　　，结论是　　　　　　　　　　　　　　　　　　 .这是一个　　　　 　命题.

5、若两圆相切，圆心距是7，其中一圆的半径为9，则另一个圆的半径为　　　　

4、圆锥的底面半径是4，母线长为5，则圆锥的侧面积等于　　　　　

3、在三张相同的卡片上标有1、2、3三个数字，从中任意抽出两张：①两张都是奇数的

概率是　　 ；②第一张为奇数，第二张为偶数的概率是　　 ；③一奇一偶的概率是

2、若a、b是方程x²+5x+3=0的实数根，则a+b=　　　　　 +=　　　 　.

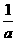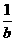1、⑴.用科学记数法表示：－0.00005478=　　　　 ⑵计算：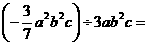　　　　　

⑶当x为　　　 时，分式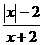的值为零；当x为　　 时，分式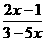的值为-1.

30.(本题满分10分)

已知一次函数y₁=2x，二次函数y₂=x²+1.

(Ⅰ)根据表中给出的x的值，计算对应的函数值y₁、y₂，并填在表格中：

(Ⅱ)观察第(Ⅰ)问中有关的数据，证明如下结论：在实数范围内，对于x的同一个值，这两个函数对应的函数值y₁≤y₂成立；

(Ⅲ)试问，是否存在二次函数y₃＝ax²+bx+c,其图像经过点(－5，2)，且在实数范围内，对于x的同一个值，这三个函数所对应的函数值y₁≤y₃≤y₂均成立，若存在，请求出该二次函数的解析式；若不存在，请说明理由。

29、动脑想一想(本大题共有2小题，共18分，只要你认真探索，仔细思考，你一定会获得成功的！)

(本题满分8分)

在日常生活中，观察各种建筑物的地板，就能发现地板常用各种正多边形地砖铺砌成美丽的图案。也就是说，使用给定的某些正多边形，能够拼成一个平面图形，既不留下一丝空白，又不互相重叠(在几何里面叫平面镶嵌)，这显然与正多边形的内角大小有关，当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角时，就拼成了一个平面图形。

根据下列图形，填写表中空格：

正多边形变边数	3	4	5	6	…	n
正多边形每个内角的度数					…

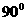如果限用一种正多边形镶嵌，哪几种正多边形能镶嵌成一个平面图形？

从正三角形、正四边形、正六边形中选一种，再在其他正多边形中选一种，请画出用两种不同的正多边形镶嵌成的一个平面图形(草图)；并探索这两种正多边形共能镶嵌成几种不同的平面图形？并说明你的理由。

28.(本题满分10分)

(1).如图将一把三角尺放在正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与线段DA相交于点E，求证：PB=PE。

(2).操作：如图，已知矩形ABCD，AD=4，DC=3。

将一把三角尺放在矩形ABCD上，并使它的直角顶点P在对角线上滑动，直角的一边始终经过B点，另一边与线段DA相交于点E。

探究①PB=PE吗？如果相等，请说明；如果不相等，请求出PB︰PE的值。

②设点P‘分别滑动到P₁、P₂时，所对应的三角形分别是△BP₁E₁、△BP₂E₂，试判断这两个三角形是否相似，请证明你的结论。(图②、③供操作，图④备用)