
题目列表(包括答案和解析)
26.(10分)市“健益”超市购进一批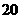 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出 千克.由销售经验知,每天销售量
千克.由销售经验知,每天销售量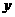 (千克)与销售单价
(千克)与销售单价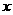 (元)(
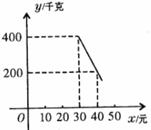
(元)(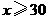 )存在如下图所示的一次函数关系.(1)试求出
)存在如下图所示的一次函数关系.(1)试求出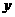 与
与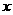 的函数关系式;
的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润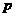 元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过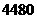 元,现该超市经理要求每天利润不得低于
元,现该超市经理要求每天利润不得低于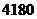 元,请你帮助该超市确定绿色食品销售单价
元,请你帮助该超市确定绿色食品销售单价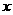 的范围(直接写出).
的范围(直接写出).
25.(8分)如图,在矩形ABCD中,对角线AC的长为10,且AB、BC(AB>BC)的长是关于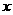 的方程
的方程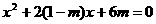 的两根。⑴求
的两根。⑴求 的值;
的值;
⑵若E是AB上一点,CF⊥DE于F,求AE为何值时,△CEF的面积是△CED的面积的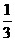 。
。
24.(8分)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。(1)若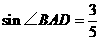 ,求CD的长;(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留
,求CD的长;(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留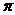 )。
)。
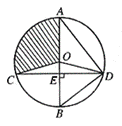
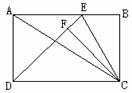
23. (9分)如图9-(1)所示,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分剪去,得到△ABF和△EDF.(1)试判断△ABF与△EDF是否全等?并加以证明.
(9分)如图9-(1)所示,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分剪去,得到△ABF和△EDF.(1)试判断△ABF与△EDF是否全等?并加以证明.
|
|
|



22.(每小题4分,共8分)
(1)解方程:(1)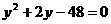 (2)解方程
(2)解方程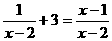
21.(每小题4分,共8分)计算:
(1)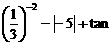 45°+
45°+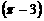 0
(2)
0
(2)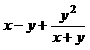
20.已知点I是锐角△ABC的内心,A1、B1、C1分别是点I关于边BC、CA、AB的对称点.若点B在△A1B1C1的外接圆上,则∠ABC的度数是 ( )
(A)90° (B)60° (C)45° (D)30°
19.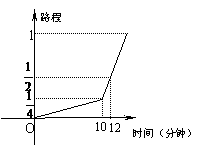 一名考生步行前往考场,10分钟走了总路程的
一名考生步行前往考场,10分钟走了总路程的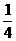 ,估计步行不能准时到达,于是他改乘租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了
( )
,估计步行不能准时到达,于是他改乘租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了
( )
(A)20分钟
(B)22分钟
(C)24分钟
(D)26分钟
18.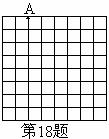 一只青蛙在如图8×8的正方形(每个小正方形的边长为1)网格的格点(小正方形的顶点)上跳跃,青蛙每次所跳的最远距离为
一只青蛙在如图8×8的正方形(每个小正方形的边长为1)网格的格点(小正方形的顶点)上跳跃,青蛙每次所跳的最远距离为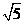 ,青蛙从点A开始连续跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是________。
,青蛙从点A开始连续跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是________。
(A)10 (B)8 (C)12 (D)9
17.关于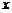 的方程
的方程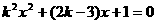 有实数根,则
有实数根,则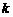 的取值范围是 ( )
的取值范围是 ( )
(A)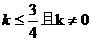 (B)
(B)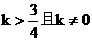
(C)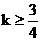 (D)
(D)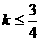
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com