
题目列表(包括答案和解析)
3、猜想证明型
(2006年大连)如图,E,F分别是平行四边形ABCD对角线BD所在直线上两点,DE=BF,请你以F为一个端点,和图中已标明字母的某一点连成一条新线段相等(只需研究一组线段相等即可)。(1)连结 ;(2)猜想 ;(3)证明(说明:写出证明过程的重要依据)。
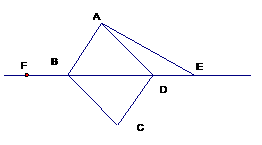
2、构造命题型
(2006年内江市)如图,在ABD和ACE中,有下列四个等式:1.AB=AC,2.AD=AE;3.∠1=∠2; 4.BD=CE. 请你以其中三个等式作为题设,余下的作为结论,写出一个真命题(要求写出已知,求证,证明及证明过程)
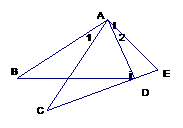
1、条件、结论开放型
(2006年攀枝花)如图点E在AB上,AC=AD,请你添加一人条件,使图中存在全等三角形,并给予证明。所添条件为 ,你得到的一对全等三角形是 。
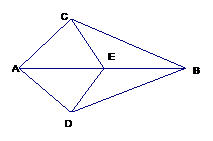
26.(本小题满分12分)
在矩形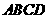 中,
中,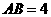 ,
,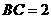 ,以
,以 为坐标原点,
为坐标原点,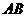 所在的直线为
所在的直线为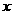 轴,建立直角坐标系.然后将矩形
轴,建立直角坐标系.然后将矩形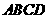 绕点
绕点 逆时针旋转,使点
逆时针旋转,使点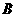 落在
落在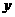 轴的
轴的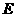 点上,则
点上,则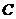 和
和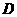 点依次落在第二象限的
点依次落在第二象限的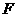 点上和
点上和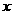 轴的
轴的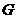 点上(如图14).
点上(如图14).
(1)求经过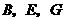 三点的二次函数解析式;
三点的二次函数解析式;
(2)设直线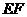 与(1)的二次函数图象相交于另一点
与(1)的二次函数图象相交于另一点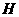 ,试求四边形
,试求四边形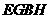 的周长.
的周长.
(3)设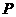 为(1)的二次函数图象上的一点,
为(1)的二次函数图象上的一点,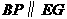 ,求
,求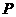 点的坐标.
点的坐标.
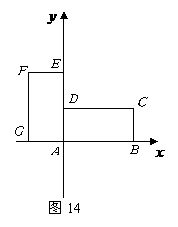
25.(本小题满分12分)
如图13,已知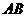 是
是 的直径,弦
的直径,弦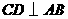 于
于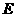 ,
,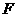 是
是 上的一点,且
上的一点,且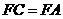 ,延长
,延长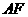 交
交 于
于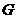 ,连结
,连结 .
.
(1)试判断 的形状(按边分类),并证明你的结论;
的形状(按边分类),并证明你的结论;
(2)若 的半径为
的半径为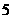 ,
,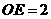 ,求
,求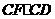 之值.
之值.
24.(本小题满分10分)
为鼓励居民节约用水和保护水资源, 市城区从2006年3月1日起,对居民生活用水采取按月按户实行阶梯式计量水价收费,其收费标准是:第一阶梯水价为
市城区从2006年3月1日起,对居民生活用水采取按月按户实行阶梯式计量水价收费,其收费标准是:第一阶梯水价为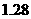 元/
元/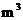 ;第二阶梯水价为
;第二阶梯水价为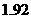 元/
元/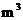 .
.
(1)每户人口为4人(含4人)以内的,月用水量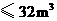 执行第一阶梯水价,月用水量
执行第一阶梯水价,月用水量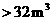 的部分执行第二阶梯水价.如果某户人口4人,3月份用水量
的部分执行第二阶梯水价.如果某户人口4人,3月份用水量 ,那么应交水费 元;4月份用水量
,那么应交水费 元;4月份用水量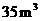 ,那么应交水费 元.
,那么应交水费 元.
(2)每户核定人数超过4人的,月用水量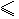 (
(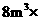 核定人数)执行第一阶梯水阶,月用水量
核定人数)执行第一阶梯水阶,月用水量 (
(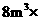 核定人数)的部分执行第二阶梯水价,若小江家人口有5人,设月用水量
核定人数)的部分执行第二阶梯水价,若小江家人口有5人,设月用水量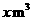 ,应交水费
,应交水费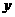 元.
元.
①请你写出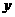 与
与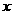 的函数关系式;
的函数关系式;
 ②若小江家某月交水费
②若小江家某月交水费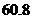 元,则该月用水量是多少
元,则该月用水量是多少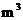 ?
?
23.(本小题满分10分)
某制衣厂近四年来关于销售额与总成本的统计图,如图11所示.
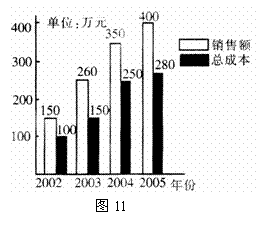
(1)请你在图12中画出四年利润(利润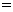 销售额
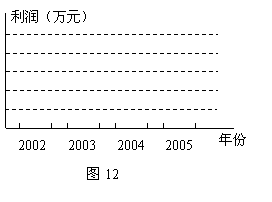
销售额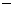 总成本)的统计直方图(要求标出数字);
总成本)的统计直方图(要求标出数字);
(2)根据图11,图12分别写出一条你发现的信息;
(3)若从2004年到2006年这两年间的利润年平均增长率相同,请你预测2006年的利润是多少万元?
22.(本小题满分8分)
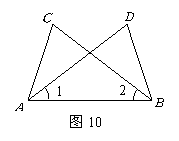
如图10,在 和
和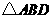 中,现给出如下三个论断:①
中,现给出如下三个论断:①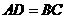 ;②
;②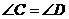 ;
;
③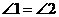 .
.
请选择其中两个论断为条件,另一个论断为结论,构造一个命题.
 (1)写出所有的真命题(写成“
(1)写出所有的真命题(写成“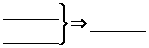 ”形式,用序号表示):
”形式,用序号表示):
.
(2)请选择一个真命题加以证明.
你选择的真命题是: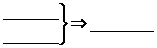 .
.
证明:
21.(本小题满分8分)
某科技馆座落在山坡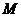 处,从山脚
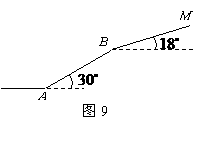
处,从山脚 处到科技馆的路线如图9所示.已知
处到科技馆的路线如图9所示.已知 处海拔高度
处海拔高度
为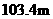 ,斜坡
,斜坡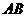 的坡角为
的坡角为 ,
,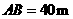 ,斜坡
,斜坡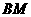 的坡角为
的坡角为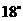 ,
,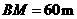 ,那么科技馆
,那么科技馆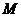 处的海拔高度是多少?(精确到
处的海拔高度是多少?(精确到 )
)
 (参考数据:
(参考数据: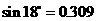
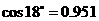
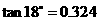
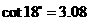 )
)
20.(本小题满分8分)
解方程: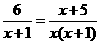 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com