
题目列表(包括答案和解析)
1.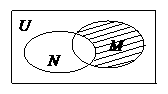 右图中矩形表示全集
右图中矩形表示全集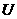 ,两个椭圆分别表示集合
,两个椭圆分别表示集合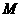 、
、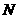 ,则阴影部分所表示的集合为
,则阴影部分所表示的集合为
 .
.
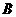 .
.
 .
.
 .
.
19.(本小题满分10分)
设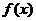 是定义在
是定义在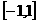 上的奇函数,且当
上的奇函数,且当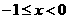 时,
时, 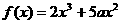
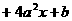 .
.
(Ⅰ)求函数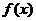 的解析式;
的解析式;
(Ⅱ) 当 时,求函数
时,求函数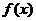 在
在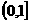 上的最大值
上的最大值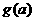 ;
;
(Ⅲ)如果对满足 的一切实数
的一切实数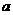 ,函数
,函数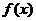 在
在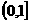 上恒有
上恒有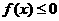 ,求实数
,求实数 的取值范围.
的取值范围.
解: (Ⅰ)当 时,
时, 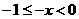 ,则
,则
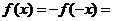
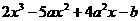 .
……………………………1分
.
……………………………1分
当 时,
时, 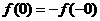
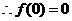 .
.
 …………………………2分
…………………………2分
(Ⅱ)当 时
时
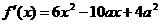
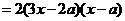
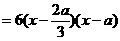 .
………3分
.
………3分
(1)当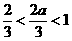 ,即
,即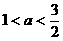 时
时
当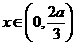 时,
时,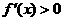 , 当
, 当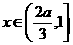 时,
时,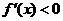 ,
,
 在
在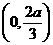 单调递增,在
单调递增,在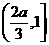 上单调递减,
上单调递减,
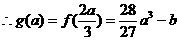 .
……………………………4分
.
……………………………4分
(2)当 ,即
,即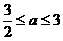 时,
时,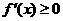 ,
,
 在
在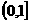 单调递增.
单调递增.
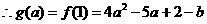 ,
……………………………5分
,
……………………………5分
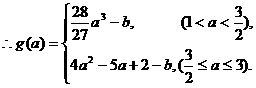 ……………………………6分
……………………………6分
(Ⅲ) 要使函数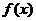 在
在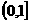 上恒有
上恒有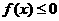 ,必须使
,必须使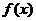 在
在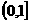 上的最大值
上的最大值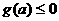 .
.
也即是对满足 的实数
的实数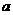 ,
,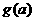 的最大值要小于或等于
的最大值要小于或等于 .
.
(1)当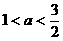 时,
时, ,此时
,此时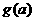 在
在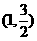 上是增函数,
上是增函数,
则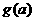
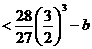
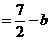 .
.
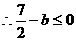 ,解得
,解得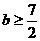 . ………①
……………………………7分
. ………①
……………………………7分
(2)当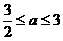 时,
时,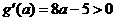
此时,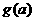 在
在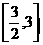 上是增函数,
上是增函数, 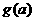 的最大值是
的最大值是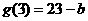 .
.
 ,解得
,解得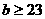 .………②
……………………………8分
.………②
……………………………8分
由①、②得实数 的取值范围是
的取值范围是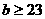 .
……………………………9分
.
……………………………9分
18.(本题满分8分)
某工厂有216名工人接受了生产1000台W型高科技产品的总任务,已知每台W型产品由4个W-1型装置和3个W-2型装置装配组成,每名工人每小时能加工6个人W-1型装置或3个W-2型装置,现将工人分成两组同时开始加工,每组分别加工一种装置.设加工W-1型装置的工人有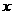 人,他们加工完成W-1型装置所需时间为
人,他们加工完成W-1型装置所需时间为 ,其余工人加工完成W-2型装置所需时间为
,其余工人加工完成W-2型装置所需时间为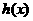 (单位:小时)
(单位:小时)
(Ⅰ)写出 、
、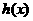 的解析式;
的解析式;
(Ⅱ)比较 与
与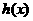 的大小,并写出这216名工人完成总任务的时间
的大小,并写出这216名工人完成总任务的时间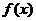 的解析式;
的解析式;
(Ⅲ)问应怎样分组,才能使完成总任务的用时最少?
解:(1)由题意可知,需加工W-1型装置4000个,加工W-2型装置3000个,所用工人分别为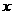 人,216
人,216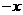 人
人
所以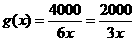 ,
,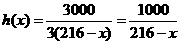 (
(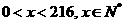 )
)
(2)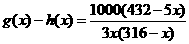
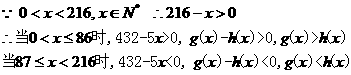
所以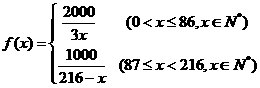
(3)完成总任务时间最少,即求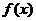 的最小值
的最小值
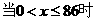 ,
,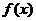 递增
递增
所以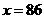 ,
,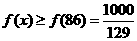 ,这时
,这时
 ,
,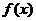 递减
递减
所以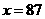 ,
, ,这时
,这时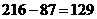
所以加工W-1型装置和加工W-2型装置的人数分别为86和130,87和129.
17.(本小题满分8分)
已知二次函数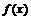 的二次项系数为
的二次项系数为 ,且方程
,且方程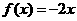 的两个实根为
的两个实根为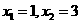
(Ⅰ)若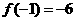 ,求
,求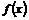 的解析式;
的解析式;
(Ⅱ)若函数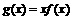 无极值,求实数
无极值,求实数 的取值范围
的取值范围
解:⑴设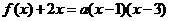
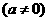 ,又
,又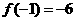
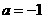 …………(2分)
…………(2分)
故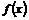 的解析式
的解析式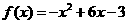 ……………3分
……………3分
⑵∴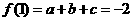 ……… ①
……… ①  ……… ②
……… ②
由①②得 ,∴
,∴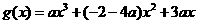 ,
,
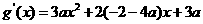 …………………………………………(5分)
…………………………………………(5分)
∵ 无极值,∴方程
无极值,∴方程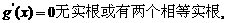 …………(6分)
…………(6分)
则
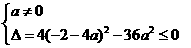 ,解得
,解得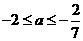 ………………(7分)
………………(7分)
故实数 的取值范围为
的取值范围为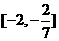 ………………………………………………(8分)
………………………………………………(8分)
16.(本小题满分8分)
已知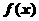 是R上的单调函数,且对任意的实数
是R上的单调函数,且对任意的实数 ,有
,有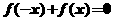 恒成立,若
恒成立,若
(Ⅰ)求
(Ⅱ)判断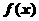 是R上的增函数还是减函数(只要写出结果,不必证明),并解关于
是R上的增函数还是减函数(只要写出结果,不必证明),并解关于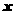 的不等式:
的不等式: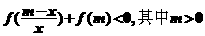
证明:(1)令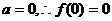
(2)由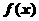 是R上的奇函数,
是R上的奇函数, ,又因
,又因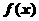 是R上的单调函数,
是R上的单调函数,
由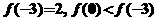 ,所以
,所以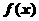 为R上的减函数.
为R上的减函数.
当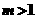 时,
时, ;
;
当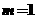 时,
时,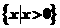
当 时,
时,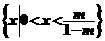 .
.
15.(本小题满分7分)
已知函数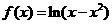 ,
,
(Ⅰ)求函数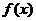 的定义域、单调递增区间;
的定义域、单调递增区间;
(Ⅱ)求函数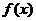 的值域.
的值域.
答案: (Ⅰ)定义域 ;递增区间为
;递增区间为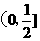
(Ⅱ)值域为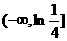
14.(本小题满分7分)
求解关于x的不等式的解集:
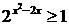
解: 
13.定义在R上的函数y=f(x)为奇函数,在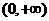 上是减函数且
上是减函数且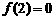 ,则
,则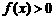 的解集为
. 答案:
的解集为
. 答案: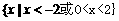 ;
;
12.如果函数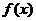 在区间D上是凸函数,则对区间D上的任意
在区间D上是凸函数,则对区间D上的任意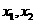 ,都有
,都有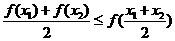 .下面函数中:
.下面函数中:
1 ,;2
,;2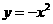 , 3
, 3 4
4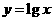
在其定义域内是凸函数的有 (填入序号)2 4
11.一次函数y=2x+4的图象与两坐标轴围成的三角形的面积为 (平方单位) 4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com