
4. (2013·贵州安顺中考)下列各数中,3.141 59,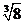 ,0.131 131 113…,-π,
,0.131 131 113…,-π,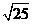 ,-
,-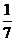 ,无理数的个数为( )www.21-cn-jy.com
,无理数的个数为( )www.21-cn-jy.com
A.1 B. 2 C.3 D.4
3.(2013·陕西中考)如果一个正比例函数的图象经过不同象限的两点A(2,m)、B(n,3),那么一定有( )21*cnjy*com
A.m>0, n>0 B.m>0, n<0C.m<0, n>0 D.m<0, n<0
2.(2013·山东威海中考)下列各式化简结果为无理数的是( )
A.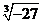 B.
B.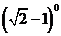 C.
C.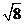 D.
D.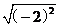
一、选择题
1. 在实数范围内,若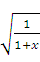 有意义,则
有意义,则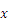 的取值范围是( )
的取值范围是( )
A. 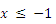 B.
B.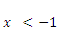 C.
C. 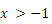 D.
D.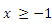
21. 本题设有(1),(2),(3)三个选考题,每题7分,请考生任选2题作答,满分14分.
如果多做,则按所做的前两题计分.作答时,先用2B铅笔在答题卡上把所选题目对应题
号右边的方框涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4—2:矩阵与变换
已知矩阵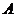 的逆矩阵
的逆矩阵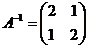 .
.
(I)求矩阵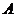 ;
;
(II)求矩阵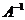 的特征值以及属于每个特征值的一个特征向量.
的特征值以及属于每个特征值的一个特征向量.
(2)(本小题满分7分)选修4—4:极坐标与参数方程
已知直线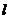 的参数方程为
的参数方程为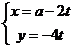 ,(
,(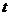 为参数),圆
为参数),圆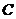 的参数方程为
的参数方程为
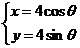 ,(
,(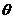 为常数).
为常数).
(I)求直线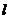 和圆
和圆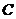 的普通方程;
的普通方程;
(II)若直线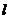 与圆
与圆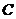 有公共点,求实数
有公共点,求实数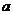 的取值范围.
的取值范围.
(3)(本小题满分7分)选修4—5:不等式选将
已知定义在R上的函数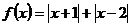 的最小值为
的最小值为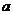 .
.
(I)求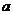 的值;
的值;
(II)若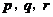 为正实数,且
为正实数,且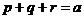 ,求证:
,求证: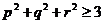 .
.
20. (本小题满分14分)
已知函数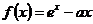 (
(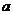 为常数)的图像与
为常数)的图像与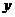 轴交于点
轴交于点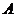 ,曲线
,曲线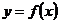 在点
在点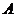 处
处
的切线斜率为-1.
(I)求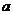 的值及函数
的值及函数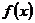 的极值;
的极值;
(II)证明:当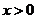 时,
时,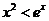 ;
;
(III)证明:对任意给定的正数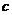 ,总存在
,总存在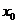 ,使得当
,使得当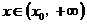 ,恒有
,恒有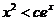 .
.
19.(本小题满分13分)
已知双曲线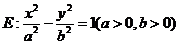 的两条渐近线分别为
的两条渐近线分别为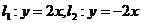 .
.
(1)求双曲线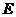 的离心率;
的离心率;
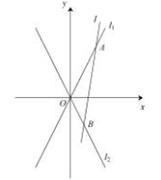
(2)如图,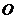 为坐标原点,动直线
为坐标原点,动直线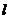 分别交直线
分别交直线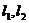 于
于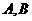 两点(
两点(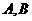 分别在第一,
分别在第一,
四象限),且 的面积恒为8,试探究:是否存在总与直线
的面积恒为8,试探究:是否存在总与直线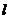 有且只有一个公
有且只有一个公
共点的双曲线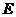 ?若存在,求出双曲线
?若存在,求出双曲线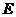 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
18.(本小题满分13分)
为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从
一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾
客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求
①顾客所获的奖励额为60元的概率
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和
50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励
总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球
的面值给出一个合适的设计,并说明理由.
17.(本小题满分12分)
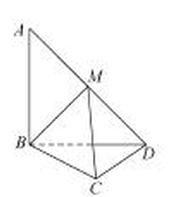
在平行四边形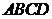 中,
中,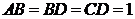 ,
,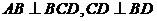 .将
.将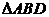 沿
沿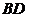 折起,使得平面
折起,使得平面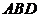
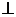 平面
平面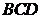 ,如图.
,如图.
(1)求证: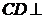
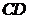 ;
;
(2)若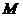 为
为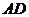 中点,求直线
中点,求直线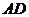 与平面
与平面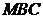 所成角的正弦值.
所成角的正弦值.
三.解答题:本大题共6小题,共80分.
16.(本小题满分13分)
已知函数 .
.
(1)若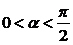 ,且
,且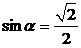 ,求
,求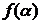 的值;
的值;
(2)求函数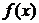 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com