
2.
若三个数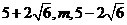 成等比数列,则m=________.
成等比数列,则m=________.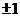
一、填空题
1.
数列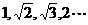 的一个通项公式为
的一个通项公式为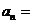 .
.
[答案]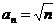
试题分析:因为数列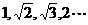 可看做
可看做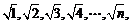 因此该数列一个通项公式为
因此该数列一个通项公式为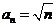 .
.
23. 宇宙深处有一颗美丽的行星,这个行星是一个半径为r(r>0)的球。人们在行星表面建立了与地球表面同样的经纬度系统。已知行星表面上的A点落在北纬60°,东经30°;B点落在东经30°的赤道上;C点落在北纬60°,东经90°。在赤道上有点P满足PB两点间的球面距离等于AB两点间的球面距离。
(1)求AC两点间的球面距离;
(2)求P点的经度;
(3)求AP两点间的球面距离。
解:设球心为O,北纬60°圈所对应的圆心为O’,
(1)那么OO’=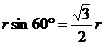 。O’A=O’C=
。O’A=O’C=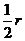 。又因为∠AO’C=60°。
。又因为∠AO’C=60°。
所以AC=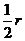 。那么∠AOC=
。那么∠AOC= (
(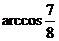 )
)
两点间的球面距离为 (
( )
)
(2)PB两点间的球面距离等于AB两点间的球面距离,所以PB=AB。
可知∠POB=∠AOB=60°,又P点在赤道上。所以P点的经度为东经90°或西经30°。
(3)显然P点的两种可能对应的AP间的球面距离相等。不妨P所在的经度为东经90°。
由条件可知O’A平行OB且等于OB的一半,延长BA与OO’交于D点,那么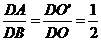 。而O’C平行OP且等于OP的一半,所以D、P、C共线且
。而O’C平行OP且等于OP的一半,所以D、P、C共线且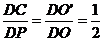 。
。
可知AC∥BP,所以A、B、C、P共面。

22. 设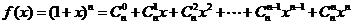 (
(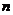 是正整数),利用赋值法解决下列问题:
是正整数),利用赋值法解决下列问题:
(1)求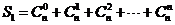 ;
;
(2)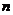 为偶数时,求
为偶数时,求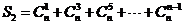 ;
;
(3)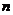 是3的倍数时,求
是3的倍数时,求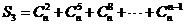 。
。
解:令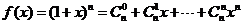 ,
,
(1)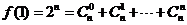 ,所以
,所以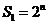
(2)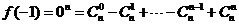 ,
,
所以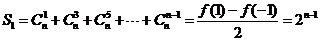
(3)记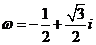 ,则
,则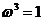 。当
。当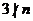 时,
时,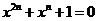 ,当
,当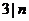 时,
时, ,
,
记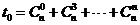 ,
,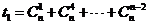 ,
,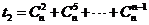
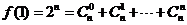 ,
,
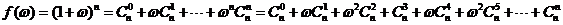 ,
,
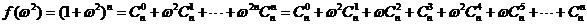
则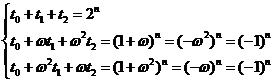
从上到下各式分别乘以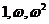 ,求得
,求得
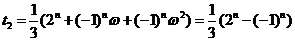 。即
。即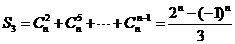
21. 已知:对于任意的多项式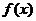 与任意复数z,
与任意复数z,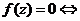
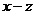 整除
整除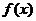 。利用上述定理解决下列问题:
。利用上述定理解决下列问题:
(1)在复数范围内分解因式: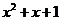 ;
;
(2)求所有满足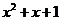 整除
整除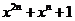 的正整数n构成的集合A。
的正整数n构成的集合A。
解:(1)令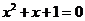 解得两个根
解得两个根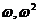 ,这里
,这里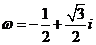
所以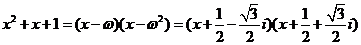
(2)记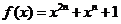 。
。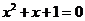 有两个根
有两个根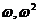 ,这里
,这里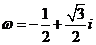 ,
,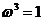
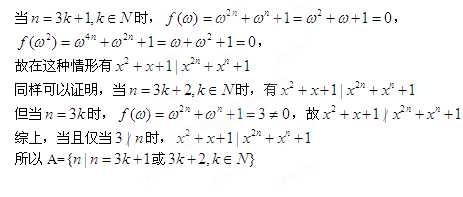
20. 如图,已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点。
(1)求证:直线AB1∥平面C1DB;
 (2)求异面直线AB1与BC1所成角的余弦值。
(2)求异面直线AB1与BC1所成角的余弦值。
证明:(1)连B C交
C交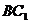 于E,连DE, 则DE∥
于E,连DE, 则DE∥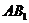 ,
,
而DE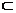 面C
面C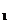 DB,
DB,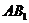
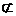 面C
面C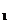 DB, ∴
DB, ∴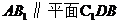
(2)由(1)知∠DEB为异面直线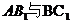 所成的角,在
所成的角,在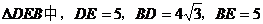
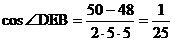 。
。
三、解答题
19. 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线。
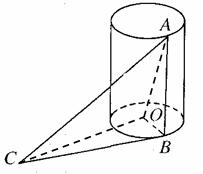 (1)求证:OB⊥AC;
(1)求证:OB⊥AC;
(2)若AC与圆柱下底面所成的角为30°,OA=2。求三棱锥A-BOC的体积。
解:(1)连结OB,由圆的切线性质有OB⊥BC,而BC是AC在底面⊙O
上的射影,∴OB⊥平面ABC,∴OB⊥AC。
(2)在RtΔOA B中,AB=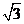 .
.
又∵∠ACB就是AC与底面⊙O所成角,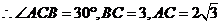 ,
,
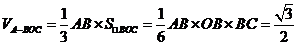
18.
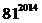 除以100的余数是 (C )
除以100的余数是 (C )
A.1 B.79 C. 21 D. 81
解: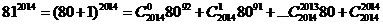
=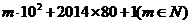
=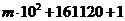 4
4
即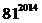 除以100的余数为21。
除以100的余数为21。
17. 三个人乘同一列火车,火车有10节车厢,则至少有2人上了同一车厢的概率为 ( B )
A.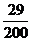 B.
B.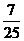 C.
C.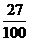 D.
D.
16. 如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为 ( A )
A.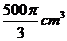 B.
B.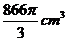 C.
C.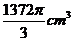 D.
D.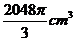
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com