
3.(2014周宁、政和一中第四次联考,21(1)) 选修4—2:矩阵与变换
已知二阶矩阵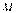 有特征值
有特征值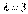 及对应的一个特征向量
及对应的一个特征向量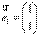 ,并且矩阵
,并且矩阵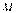 对应的变换将点
对应的变换将点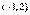 变换成
变换成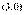 ,求矩阵
,求矩阵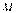 .
.
[解析] 3. 设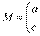
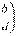 ,有已知得
,有已知得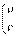
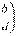

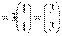 ,
,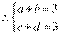 ,
,
又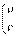
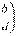
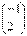
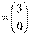 ,
,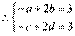 ,
,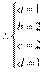 ,
,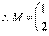
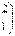 .
(7分)
.
(7分)
2.(2014福州高中毕业班质量检测, 21(1)) 选修4-2:矩阵与变换.
已知矩阵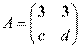
 , 若矩阵A属于特征值6的一个特征向量为
, 若矩阵A属于特征值6的一个特征向量为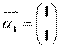 ,属于特征值1的一个特征向量
,属于特征值1的一个特征向量 .
.
(Ⅰ)求矩阵A的逆矩阵;
(Ⅱ)计算
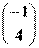 的值.
的值.
[解析] 2.(Ⅰ) 法一: 依题意, 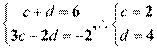 .
. 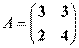 .
.
所以 . (4分)
. (4分)
法二: 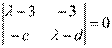 ,即
,即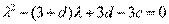 的两个根为6和1,
的两个根为6和1,
故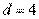 ,
, 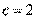 .
. 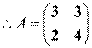 ,所以
,所以 ,
,
(Ⅱ) 法一: 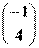 =2
=2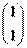 -
- ,A3
,A3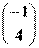 =2×63
=2×63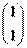 -13
-13 =
=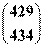 . (7分)
. (7分)
法二: 

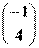 =
=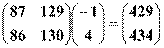 . (7分)
. (7分)
1.(2013福建厦门高三一月质量检查,15,5分)(1)(矩阵与变换选做题)已知矩阵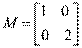 ,
,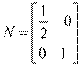 ,曲线y=sinx在矩阵MN对
,曲线y=sinx在矩阵MN对 应的变换作用下得到曲线C,则C的方程是 .
应的变换作用下得到曲线C,则C的方程是 .
[解析] 1.MN=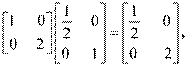 所以在矩阵MN变换下
所以在矩阵MN变换下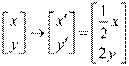 ,则
,则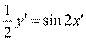 ,即
,即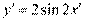 ,所以曲线
,所以曲线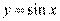 在矩阵MN变换下得到曲线C的方程是
在矩阵MN变换下得到曲线C的方程是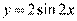 .
.
5.若a,b,c为△ABC的三边,且关于x的方程
4x2+4(a2+b2+c2)x+3(a2b2+b2c2+c2a2)=0有两个相等的实数根,试证△ABC是等边三角形.
4.若方程x2+ax+b=0和x2+bx+a=0有一个公共根,求(a+b)2000的值.
3.若对任何实数a,关于x的方程
x2-2ax-a+2b=0
都有实数根,求实数b的取值范围.
2.解下列关于x的方程:
(1)abx2-(a4+b4)x+a3b3=0;
(2)(2x2-3x-2)a2+(1-x2)b2=ab(1+x2).
1.解方程:
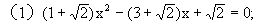
(2)20x2+253x+800=0;
(3)x2+|2x-1|-4=0.
高二数学试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,其中第II卷中第22和23题为选考题,其他题为必考题。考生作答时,将答案答在答题卡上,在本试卷上答题无效。
24.(12分)如图1,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),
且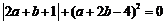 .(1)求a,b的值;
.(1)求a,b的值;
(2)①在x轴的正半轴上存在一点M,使S△COM=△ABC的面积,
求出点M的坐标;
②在坐标轴的其它位置是否存在点M,使△COM的面积=△ABC的面积仍然成立,若存在,请直接写出符合条件的点M的坐标为
 (3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE.当点P运动时,
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上一动点,连接OP,OE平分∠AOP,OF⊥OE.当点P运动时,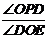 的值是否会改变?若不变,求其值;若改变,说明理由.
的值是否会改变?若不变,求其值;若改变,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com