
16. (2014贵州贵阳高三适应性监测考试, 22) [选修4-1:几何证明选讲]
如图,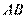 是圆
是圆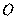 的直径,弦
的直径,弦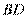 、
、 的延长线相交于点
的延长线相交于点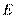 ,
,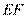 垂直
垂直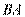 的延长线于点
的延长线于点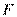 .
.
(Ⅰ)求证: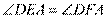 ;
;
(Ⅱ) 求证: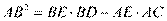 .
.
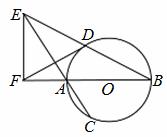
[解析] 16.(Ⅰ)连结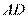 ,因为
,因为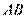 为圆的直径,
为圆的直径,
所以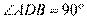 ,又
,又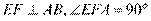 ,
,
则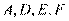 四点共圆,
四点共圆,
所以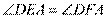 . (5分)
. (5分)
(Ⅱ)由(Ⅰ)知,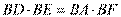 ,连结
,连结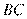 ,
,
又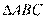 ∽
∽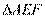 ,所以
,所以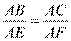
即 ,
,
所以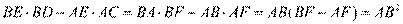 . (10分)
. (10分)
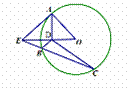
15. (2014河北唐山高三第一次模拟考试,22) 选修4―1: 几何证明选讲
如图,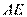 是圆
是圆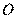 的切线,
的切线, 是切点,
是切点,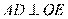 于
于 ,过点
,过点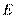 的割线交圆
的割线交圆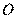 于
于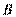 、
、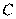 两点.
两点.
(Ⅰ)证明: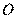 ,
, ,
,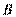 ,
,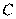 四点共圆;
四点共圆;
(Ⅱ)设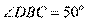 ,
,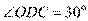 ,求
,求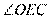 的大小.
的大小.
[解析] 15.(Ⅰ)连结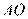 ,则
,则 . 由射影定理得
. 由射影定理得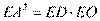 ,
,
由切割线定理得 ,故
,故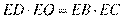 ,即
,即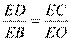 ,
,
又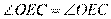 ,所以
,所以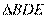 ~
~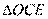 ,所以
,所以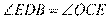 .
.
因此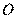 ,
, ,
,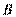 ,
,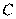 四点共圆. (6分)
四点共圆. (6分)
(Ⅱ)连结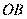 . 因为
. 因为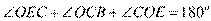 ,结合(Ⅰ)得
,结合(Ⅰ)得
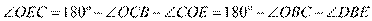
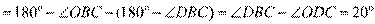 . (10分)
. (10分)
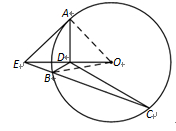
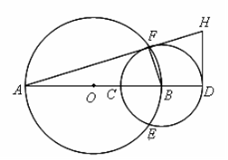
14. (2014河北石家庄高中毕业班复习教学质量检测(二),22) 选修4—1:几何证明选讲:如图,已知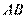 为圆
为圆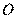 的一条直径,以端点
的一条直径,以端点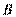 为圆心的圆交直线
为圆心的圆交直线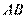 于
于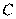 、
、 两点,交圆
两点,交圆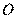 于
于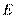 、
、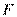 两点,过点
两点,过点 作垂直于
作垂直于 的直线,交直线
的直线,交直线 于
于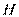 点.
点.
(Ⅰ)求证: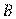 、
、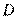 、
、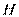 、
、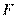 四点共圆;
四点共圆;
(Ⅱ)若 ,
,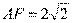 , 求
, 求 外接圆的半径.
外接圆的半径.
[解析] 14.(Ⅰ)因为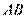 为圆
为圆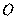 一条直径,所以
一条直径,所以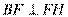 ,又
,又 ,
,
故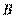 、
、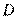 、
、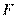 、
、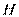 四点在以
四点在以 为直径的圆上,
为直径的圆上,
所以,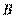 、
、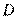 、
、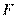 、
、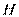 四点共圆. (4分)
四点共圆. (4分)
(Ⅱ)因为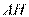 与圆
与圆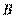 相切于点
相切于点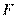 ,由切割线定理得
,由切割线定理得
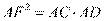 , 即
, 即 ,
,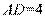 ,
,
所以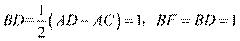
又 ,
,
则 , 得
, 得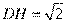 ,
,
连接 , 由(1)可知
, 由(1)可知 为
为 的外接圆直径,
的外接圆直径,
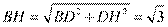 , 故
, 故 的外接圆半径为
的外接圆半径为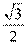 . (10分)
. (10分)
13. (2014山西太原高三模拟考试(一),22) 选修4一1:几何证明选讲
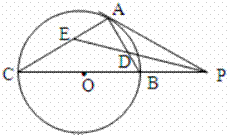
如图,已知PA与⊙O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB、AC于点D、E.
(Ⅰ)证明:∠ADE=∠AED;
(Ⅱ)若AC=AP,求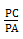 的值.
的值.
[解析] 13.


12. (2014山西忻州一中、康杰中学、临汾一中、长治二中四校高三第三次联考,2 2) 选修4-1:几何证明选讲
2) 选修4-1:几何证明选讲
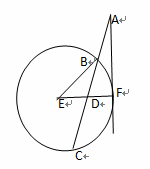
如图,过圆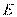 外一点
外一点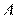 作一条直线与圆
作一条直线与圆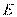 交于
交于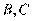 两点,且
两点,且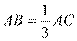 ,作直线
,作直线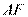 与圆
与圆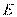 相切于点
相切于点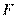 ,连结
,连结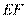 交
交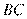 于点
于点 ,已知圆
,已知圆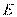 的半径为2,
的半径为2,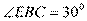
(1)求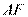 的长;
的长;
(2)求证: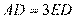 .
.
[解析] 12.(1)延长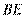 交圆
交圆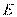 于点
于点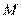 ,连结
,连结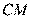 ,
,
则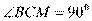 ,
,
又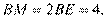
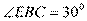 ,所以
,所以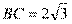 ,
,
又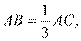 可知
可知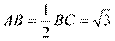 ,所以
,所以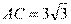
根据切割线定理得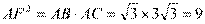 ,即
,即
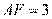 .
.
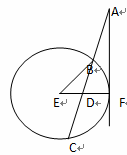
⑾证明:过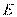 作
作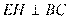 于
于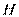 ,则
,则 ,
,
从而有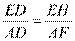 ,又由题意知
,又由题意知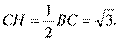

所以 ,因此
,因此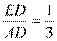 ,即
,即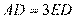
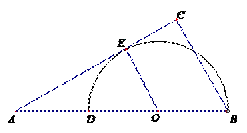
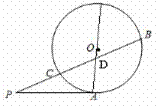
11. (2014重庆五区高三第一次学生调研抽测,14) 如图,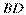 是半圆
是半圆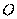 的直径,
的直径,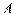 在
在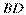 的延长线上,
的延长线上,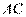 与半圆相切于点
与半圆相切于点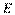 ,
,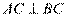 ,若
,若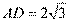 ,
,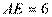 ,则
,则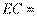 .
.
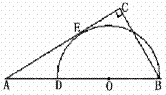
[解析] 11. 延长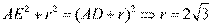 ,又
,又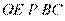 ,所以
,所以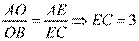 .
.
10.(2014湖北八校高三第二次联考数学(理)试题,15)(选修4-1:几何证明选讲)
如图,△ABC为圆的内接三角形,BD为圆的弦,且BD//AC. 过点A 作圆的切线与DB的延长线交于点E, AD与BC交于点F.若AB = AC,AE
=
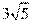 , BD = 4,则线段CF的长为______.
, BD = 4,则线段CF的长为______.
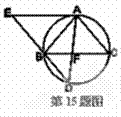
[解析] 10. 根据切割线定理可得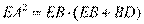 ,代入数据得EB=5. 因为AB=AC,可得∠C=∠ABC,又因为EA是切线,根据同弧对应的圆周角相等可得,∠C=∠EAB,所以可得∠EAB=∠ABC,所以可得EA//BC,又因为BE//AC,所以四边形ACBE为平行四边形,所以AC=EB=5,BC=EA=
,代入数据得EB=5. 因为AB=AC,可得∠C=∠ABC,又因为EA是切线,根据同弧对应的圆周角相等可得,∠C=∠EAB,所以可得∠EAB=∠ABC,所以可得EA//BC,又因为BE//AC,所以四边形ACBE为平行四边形,所以AC=EB=5,BC=EA=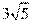 . 因为AC//BD,所以可得弧AB与弧CD相等,所以可得∠FACA=∠ACB,所以△AFC∽△BAC,可得
. 因为AC//BD,所以可得弧AB与弧CD相等,所以可得∠FACA=∠ACB,所以△AFC∽△BAC,可得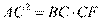 ,代入数据得
,代入数据得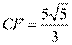 .
.
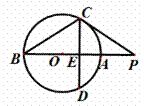
9. (2014重庆铜梁中学高三1月月考试题,16) 如图, 切⊙O于点
切⊙O于点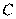 ,割线
,割线 经过圆心
经过圆心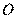
 ,弦
,弦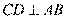 于点
于点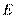 ,
,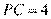
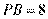 ,则
,则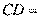 _________.
_________.
[解析] 9. 依题意,由切割线定理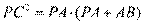 ,所以
,所以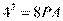 ,即
,即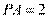 ,所以圆的半径
,所以圆的半径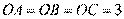 ,由
,由 为切线,所以
为切线,所以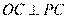 ,所
,所 以
以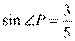 ,又弦
,又弦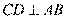 于点
于点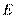 ,所以
,所以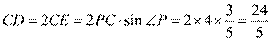 .
.
8. (2014北京东城高三第二学期教学检测,10) 如图, 与圆
与圆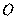 相切于
相切于 ,不过圆心
,不过圆心 的割线
的割线 与直径
与直径 相交于
相交于 点. 已知∠
点. 已知∠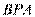 =
=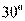 ,
,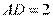 ,
,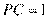 , 则圆
, 则圆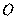 的半径等于_______.
的半径等于_______.
[解析] 8.由题意可得: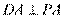 , 又因为
, 又因为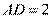 ,
, ,所以
,所以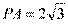 ,
,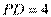 . 从而
. 从而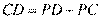
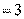 。由切割线定理
。由切割线定理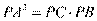 可得
可得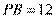 ,所以
,所以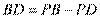
 . 再由相交弦定理
. 再由相交弦定理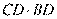
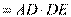 ,所以
,所以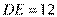 . 故直径
. 故直径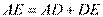
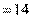 ,从而半径为7.
,从而半径为7.
7. (2014广东广州高三调研测试,14) (几何证明选讲选做题)
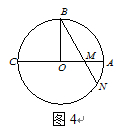
如图4,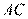 为⊙
为⊙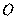 的直径,
的直径,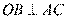 ,弦
,弦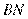 交
交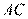 于点
于点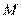 . 若
. 若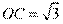 ,
,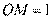 ,则
,则
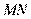 的长为_______.
的长为_______.
[解析] 7. 由已知可得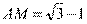 ,
,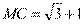 ,
,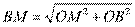
 ,由相交弦定理得:
,由相交弦定理得: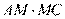
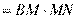 ,所以
,所以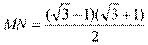
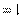
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com