
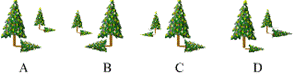
2.下列四幅图形中,表示两颗圣诞树在同一时刻阳光下的影子的图形可能是( )
下列各题中均有四个备选答案,其中有且只有一个答案是正确的,请在答题卡上把正确答案的代号涂黑。
1.一元二次方程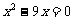 的解是( )
的解是( )
A.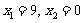 B.
B.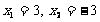
C.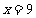 D.
D.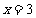
25.(本小题满分14分)
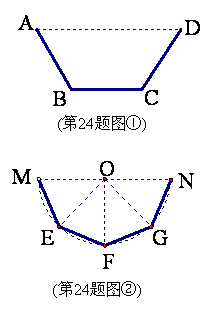
某中学一课外学习小组探究这样一个问题:现有一个长为2米,宽为60㎝的长方形铁片,要把它扎制成一个长2米且两边开口的过水槽,试设计出使水槽能通过水的流量最大的扎制方案.
经过讨论,小组成员达成共识:在水流速度一定的情况下,水槽的横截面积越大,则通过水槽的流量越大.现假定你是该小组的成员,参与他们的探索活动:
(1)方案甲,如图①把铁片扎制成等腰梯形水槽,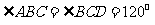 . 设
. 设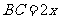 ㎝,梯形
㎝,梯形 (水槽的横截面)的面积为
(水槽的横截面)的面积为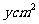 ,试写出
,试写出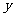 关于
关于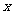 的函数关系式以及自变量
的函数关系式以及自变量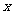 的取值范围,并求出
的取值范围,并求出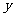 的最大值;
的最大值;
(2)小组成员王芳同学进一步探究后说:“方案乙: 把水槽的横截面扎制成如图②所示的形状,其中点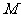 、
、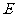 、
、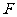 、
、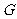 、
、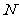 在以
在以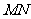 为直径的半圆周上,
为直径的半圆周上,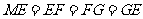 =
=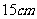 .此时,截面
.此时,截面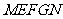 的面积
的面积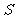 比方案甲中
比方案甲中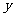 的最大值更大”,她的说法正确吗?为什么?
的最大值更大”,她的说法正确吗?为什么?
(3)你能找到一种使水槽的横截面面积比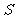 更大的设计方案吗?若能,请画出图形,标出必要的数据(可不写解答过程),写出你所设计方案的横截面面积;若不能,请说明理由。
更大的设计方案吗?若能,请画出图形,标出必要的数据(可不写解答过程),写出你所设计方案的横截面面积;若不能,请说明理由。
24.(本小题满分14分)
如图,点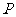 、
、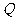 分别为等边
分别为等边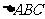 的两边
的两边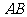 和
和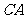 上的两个动点,
上的两个动点,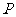 、
、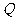 分别以相同的速度由
分别以相同的速度由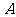 向
向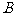 和由
和由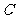 向
向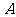 运动(不与端点重合),设
运动(不与端点重合),设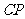 与
与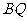 相交于
相交于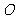 .
.
 (1)比较
(1)比较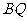 与
与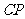 长的大小关系,并给予证明.
长的大小关系,并给予证明.
(2)当点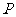 、
、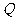 运动到何处时,
运动到何处时,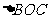 的周长
的周长
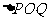 的周长的2倍?为什么?
的周长的2倍?为什么?
(3)探究点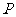 、
、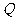 在运动过程中
在运动过程中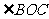 的大小怎样变化?
的大小怎样变化?
并对你的结论给予证明.
23. (本小题满分12分)
为了缓解电力紧张局面,电力公司鼓励工厂错峰用电,规定:每天0:00至7:00的时间为用电平稳时段,电价为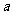 元/度,每天7:00至24:00为用电高峰时段,电价为
元/度,每天7:00至24:00为用电高峰时段,电价为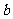 元/度.下表是红梅钢铁厂今年2、3月份的用电量与电费情况统计表:
元/度.下表是红梅钢铁厂今年2、3月份的用电量与电费情况统计表:
|
月份 |
用电量(万度) |
电费(万元) |
|
2 |
12 |
9.6 |
|
3 |
16 |
13.2 |
 (1)若2月份平稳时段的用电量占当月总用电量的
(1)若2月份平稳时段的用电量占当月总用电量的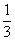 ,3月份平稳时段的用电量占当月总用电量的
,3月份平稳时段的用电量占当月总用电量的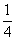 ,试求电价
,试求电价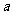 、
、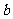 的值.
的值.
(2)该钢铁厂4月份计划用电20万度,要使电费支出不超过15万元,应如何安排用电计划?
22. (本小题满分12分)
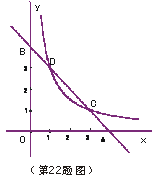 如图,已知直线
如图,已知直线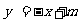 与双曲线
与双曲线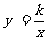 (
( )相交于C、D两点,且点C的坐标为
)相交于C、D两点,且点C的坐标为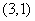 .
.
(1)求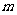 的值和双曲线的解析式;
的值和双曲线的解析式;
(2)观察直线的图象写出: 当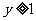 时,
时,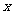 的取值范围;
的取值范围;
(3)观察双曲线的图象写出:当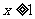 时,
时,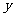 的取值范围.
的取值范围.
21. (本小题满分12分)
(本小题满分12分)
某高级中学高一年级共
有1141名同学,今年一月
参加了广州市数学质量
抽测,右图是学生测试
成绩的统计图(分数全
是整数,满分120分).
请根据以上信息完成
下列问题:
(1) 试将统计图补
充完整;
(2)求学生成绩的中位数落在哪一个分数段内?
(3)以90分(含90)以上的成绩定为优秀,据统计广州此次质量抽测的优秀率((优秀人数÷总人数)×100%))为25%,试问该中学此次高一成绩的优秀率超过全市平均水平多少个百分点?
20.(本小题满分10分)
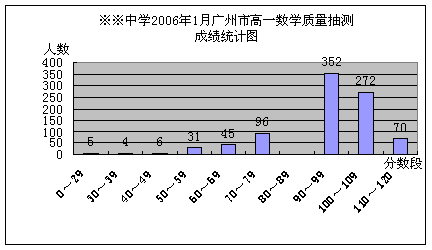
如图,AB切⊙O于点B,OA交⊙O于C点,过C作DC⊥OA交AB于D,且BD:AD=1:2
 (1)求
(1)求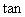 A的值.
A的值.
(2)若OC =1,求AB及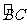 的长.
的长.
19.(本小题满分10分,每小题5分)
(1)在实数范围内分解因式:
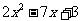 .
.
(2)解不等式组: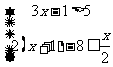 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.

18.(本小题满分9分)
在南区公园的一片开阔草地中有一个小湖,在小湖的两侧各有一棵大树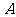 、
、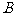 ,现要测量出
,现要测量出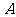 、
、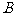 间的距离,但无法直接丈量.秦明同学用所学勾股定理的知识,设计了一种测量方案:
间的距离,但无法直接丈量.秦明同学用所学勾股定理的知识,设计了一种测量方案:
如图①,在草地上选取一点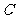 ,使点
,使点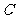 到点
到点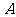 、
、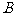 间的距离可测量,且
间的距离可测量,且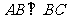 ,丈量出
,丈量出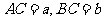 ,则由勾股定理得:
,则由勾股定理得: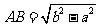 .
.
试利用你所学过的数学知识,再设计出两种不同的测量方案(要求:画出草图,写出计算公式,并标明公式中每个字母的实际意义).

.
解:方案一:
方案二:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com