25.(本题满分12分)

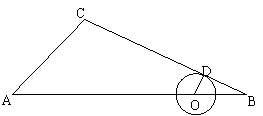
如图，在△ABC中，AB＝17，AC＝5，∠CAB＝45°，点O在BA上移动，以O为圆心作⊙O，使⊙O与边BC相切，切点为D，设⊙O的半径为x，四边形AODC的面积为y．

　　 ⑴ 求 y与x的函数关系式；

　　 ⑵ 求x的取值范围；

　　 ⑶ 当x为何值时，⊙O与BC、AC都相切？

24.(本题满分12分)

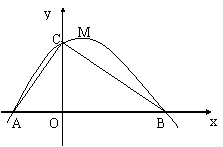
如图，函数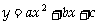(其中a，b，c为常数)的图象分别与x轴，y轴交于A，B，C三点，M为抛物线的顶点，且AC⊥BC，OA＜OB．

⑴ 试确定a，b，c的符号；

⑵ 求证：b²－4ac＞4；

⑶ 当b ＝2时，M点与经过A，B，C三点的圆的位置关系如何？证明你的结论．

注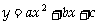：的对称轴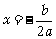为，顶点为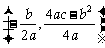

23.(本题满分10分)

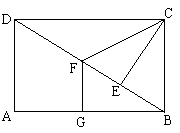
如图，已知矩形ABCD中，CE⊥BD于E，CF平分∠DCE与DB交于点F，FG∥DA与AB交于点G．　

⑴　 求证：BF＝BC；

⑵　若AB＝4 cm，AD＝3cm，求CF．　　　

22.(本题满分10分)

丰华中学为了解初三男生的身高情况，抽测了50名男生的身高，数据如下：(单位：米)

⑴　若将数据分成6组，取组距为0.04米，试完成相应的频率分布表：

⑵　补全频率分布直方图：

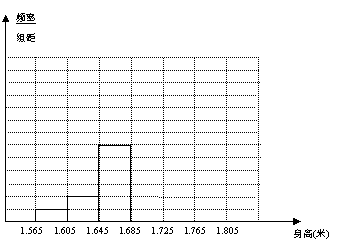
⑶　根据样本数据，估计该校初三男生的平均身高约为　　　米；身高在1.695~1.755米之间的男生所占的百分比为　　　，如果该校初三共有450名男生，那么在1.695~1.755米之间的人数约为　　　　　 人．

21.(本题满分10分)

某家庭新购住房需要装修，如果甲、乙两个装饰公司合做，12天可以完成，需付装修费1.04万元；如果甲公司先做9天，剩下的由乙公司来做，还需16天完成，共需付装修费1.06万元．若只选一个装饰公司来完成装修任务，应选择哪个装饰公司？试说明理由．

20.(本题满分8分)

为美化环境，某单位需要在一块正方形空地上分别种植四种不同的花草，计划将这块空地按如下要求分成四块：⑴分割后的整个图形必须是中心对称图形；⑵四块图形的形状相同；⑶四块图形的面积相等．

　 　请按照上述三个要求，分别在下面的正方形中给出4种不同的分割方法．

(尺规或徒手作图均可，但要尽可能准确、美观些，不写画法)

19.(每小题6分，满分12分)

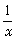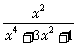⑴　已知x+＝3，求的值．

⑵　已知关于x的一元二次方程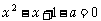有两个不相等的正根，求a的取值范围．

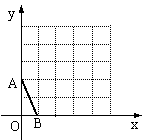
18. 在方格纸中，每个小格的顶点称为格点，以格点为顶点的三角形叫做格点三角形．在如图5×5的方格纸中，以A、B为顶点作格点三角形与△OAB相似(相似比不能为1)，则另一个顶点C的坐标为　　　　　 　．

17. 下面是用棋子摆成的“上”字型图案：

按照以上规律继续摆下去，通过观察，可以发现：(1)第五个“上”字需用　　　　 枚棋子；(2)第n个“上”字需用　 　　　　枚棋子．

16. 解方程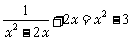时，若设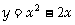，则原方程可化为一元二次方程的一般形式是　　　　　　 　　　 　．