
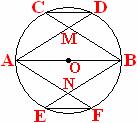
17. 如图, AB是⊙O的直径, C、E是圆周上关于AB对称的两个不同点, CD//AB//EF, BC与AD交于M, AF与BE交于N. 在A、B、C、D、E、F、M、N中, 能构成矩形的四个点有
A. C、E、F、D B. A、E、B、D C. A、F、B、C D. A、M、B、N
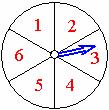
16. 如图所转盘被划分成六个相同大小的扇形, 并分别标出1、2、3、4、5、6这六个数字, 指针停在每个扇形的可能性相等, 四位同学各自发表了下述见解:
甲: 如果指针前三次都停在了3号扇形, 下次就一定不会停在3号扇形了;
乙: 只要指针连续转六次, 一定会有一次停在6号扇形;
丙: 指针停在奇数号扇形的概率和停在偶数号扇形的概率相等;
丁: 运气好的时候, 只要在转动前默默想好让指针停在6号扇形, 指针停在6号扇形的可能性就会加大.
其中你认为错误的见解有
A. 甲 B. 乙 C. 丙 D. 丁
(第16题图) (第17题图)
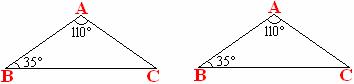
15. (6分) 如图, 在△ABC中, ∠A=1100, ∠B=350, 请你应用变换的方法得到一个三角形使它与△ABC全等, 且要求得到的三角形与原△ABC组成一个四边形.
(1)要求用两种变换方法解决上述问题;(写出变换名称, 画出图形即可)
(2)指出四边形是什么图形? (不要求证明)
说明: 如果两种平移变换方法解决此题算一种变换; 两种变换是指平移、旋转等不同变换.
14. (6分) 小明在银行存入一笔零花钱. 已知这种储蓄的年利率为n%, 若设到期后的本息和(本金+利息)为y (元), 存入的时间为x (年), 那么
(1)下列哪个图象更能反映y与x之间的函数关系? 从图中你能看出存入的本金是多少元? 一年后的本息和是多少元?
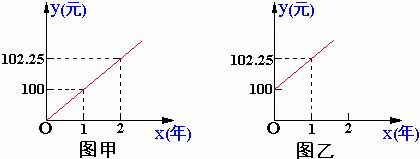
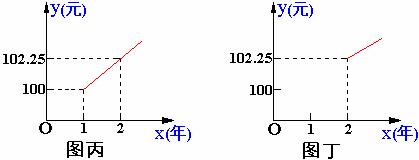
(2)根据(1)的图象, 求出y与x的函数关系式(不要求写出自变量x的取值范围), 并求出两年后的本息和.
13.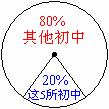 (8分) 黄冈市从2006年年初取消初中生上早晚自习后, 学生的综合素质状况受到全社会的广泛关注. 黄冈市有关部门对全市初中九年级9200名学生数学学业考试状况进行了一次抽样调查, 从中随机抽查了5所初中九年级全体学生的数学调考成绩, 右图是2006年3月抽样情况统计图. 这5所初中的九年级学生的得分情况如下表(数学学业考试满分120分)
(8分) 黄冈市从2006年年初取消初中生上早晚自习后, 学生的综合素质状况受到全社会的广泛关注. 黄冈市有关部门对全市初中九年级9200名学生数学学业考试状况进行了一次抽样调查, 从中随机抽查了5所初中九年级全体学生的数学调考成绩, 右图是2006年3月抽样情况统计图. 这5所初中的九年级学生的得分情况如下表(数学学业考试满分120分)
(1)这5所初中九年级学生的总人数有多少人?
(2)统计时, 老师漏填了表中空白处的数据, 请你帮老师填上:
|
分数段 |
频数 |
频率 |
|
72分以下 |
736 |
0.4 |
|
72-80分 |
276 |
0.15 |
|
81-95分 |
|
|
|
96-108分 |
300 |
0.2 |
|
109-119分 |
|
|
|
120分 |
5 |
(3)随机抽取一人, 恰好是获得120分的概率是多少?
(4)从上表中, 你还能获得其他的信息吗? (写出一条即可)
12. 在5×5方格纸中将图甲中的图形N平移后的位置如图乙所示, 那么正确的平移方法是
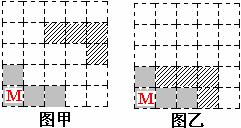
A. 先向下移动1格, 再向左移动1格 B. 先向下移动1格, 再向左移动2格
C. 先向下移动2格, 再向左移动1格 D. 先向下移动2格, 再向左移动2格
11. 如图所示的函数图象的关系式可能是
A.
y=x B.
y=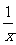 C.
y=x2 D.
y=
C.
y=x2 D.
y=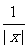
10. 如上右图是跷跷板的示意图, 支柱OC与地面垂直, 点O是横板AB的中点, AB可可绕着点O上下转动, 当A端落地时, ∠OAC=200, 横板上下可转动的最大角度(即∠A’OA)是
A. 800 B. 600 C. 400 D. 200
9. 如下左图是一个立方体图形的二视图, 根据图示的数据求出这个立方体图形的体积是
A.
24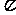 cm3 B.
48
cm3 B.
48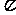 cm3 C.
72
cm3 C.
72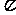 cm3 D.
192
cm3 D.
192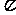 cm3
cm3
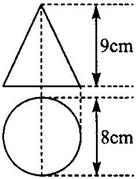
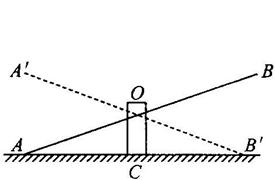
(第9题图) (第10题图)
8. 下列四幅图形中, 表示两棵小树在同一时刻阳光下的影子的图形可能是

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com