
5. 如图,在
如图,在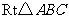 中,
中,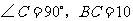 米,
米,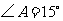 ,
,
用科学计算器算得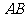 的长约为 米.(精确到
的长约为 米.(精确到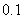 米)
米)
4. 六一儿童节期间,佳明眼镜店开展优惠学生配镜的活动,某款式眼镜的广告如图,请你为广告牌补上原价.
六一儿童节期间,佳明眼镜店开展优惠学生配镜的活动,某款式眼镜的广告如图,请你为广告牌补上原价.

3.小明设计了一个关于实数的运算程序如下,当输入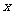 的值为
的值为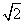 时,则输出的数值为 .
时,则输出的数值为 .

2.分解因式: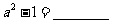 .
.
1. 的相反数是 .
.
28.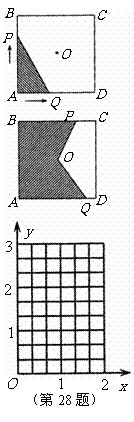 如图,正方形
如图,正方形 的边长为
的边长为 ,在对称中心
,在对称中心 处有一钉子.动点
处有一钉子.动点 ,
, 同时从点
同时从点 出发,点
出发,点 沿
沿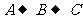 方向以每秒
方向以每秒 的速度运动,到点
的速度运动,到点
 停止,点
停止,点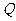 沿
沿 方向以每秒
方向以每秒 的速度运动,到点
的速度运动,到点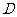 停止.
停止.
 ,
,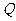 两点用一条可伸缩的细橡皮筋联结,设
两点用一条可伸缩的细橡皮筋联结,设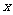 秒后橡皮筋扫过的
秒后橡皮筋扫过的
面积为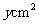 .
.
(1)当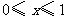 时,求
时,求 与
与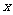 之间的函数关系式;
之间的函数关系式;
(2)当橡皮筋刚好触及钉子时,求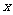 值;
值;
(3)当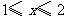 时,求
时,求 与
与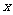 之间的函数关系式,并写出橡皮筋从
之间的函数关系式,并写出橡皮筋从
触及钉子到运动停止时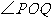 的变化范围;
的变化范围;
(4)当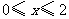 时,请在给出的直角坐标系中画出
时,请在给出的直角坐标系中画出 与
与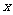 之间的
之间的
函数图象.
27.如图,在平面直角坐标系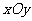 中,把矩形
中,把矩形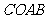 绕点
绕点 顺时针旋转
顺时针旋转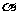 角,得到矩形
角,得到矩形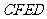 .设
.设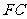 与
与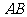 交于点
交于点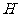 ,且
,且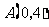 ,
,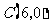 (如图1).
(如图1).
(1)当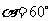 时,
时,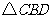 的形状是_____________;
的形状是_____________;
(2)当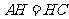 时,求直线
时,求直线 的解析式;
的解析式;
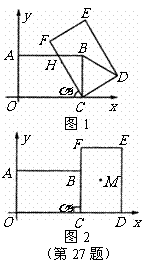 (3)当
(3)当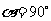 时,(如图2).请探究:经过点
时,(如图2).请探究:经过点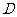 ,且以点
,且以点 为顶点的抛物线,是否经过矩形
为顶点的抛物线,是否经过矩形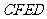 的对称中心
的对称中心 ,并说明理由.
,并说明理由.
26.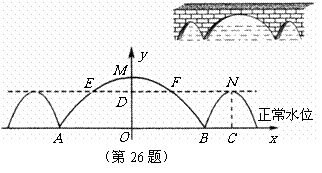 如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度
如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度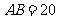 米,顶点
米,顶点 距水面
距水面 米(即
米(即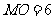 米),小孔顶点
米),小孔顶点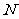 距水面
距水面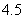 米(即
米(即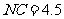 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度
米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,求此时大孔的水面宽度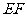 .
.
25.如图,在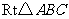 和
和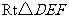 中,
中,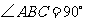 ,
,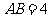 ,
,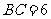 ,
,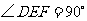 ,
,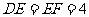 .
.
(1)移动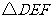 ,使边
,使边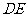 与
与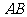 重合(如图1),再将
重合(如图1),再将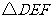 沿
沿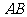 所在直线向左平移,使点
所在直线向左平移,使点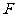 落在
落在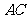 上(如图2),求
上(如图2),求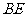 的长;
的长;
(2)将图2中的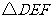 绕点
绕点 顺时针旋转,使点
顺时针旋转,使点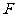 落在
落在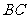 上,连结
上,连结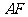 (如图3).请找出图中的全等三角形,并说明它们全等的理由.
(如图3).请找出图中的全等三角形,并说明它们全等的理由.
(不再添加辅助线,不再标注其它字母).
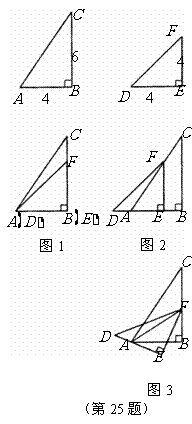
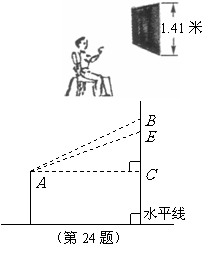
24.如图,小刚面对黑板坐在椅子上.若把黑板看作矩形,其上的一个字看作点 ,过点
,过点 的该矩形的高为
的该矩形的高为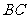 ,把小刚眼睛看作点
,把小刚眼睛看作点 .现测得:
.现测得: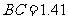 米,视线
米,视线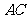 恰与水平线平行,视线
恰与水平线平行,视线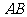 与
与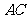 的夹角为
的夹角为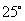 ,视线
,视线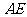 与
与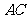 的夹角为
的夹角为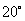 .
.
求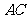 和
和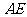 的长(精确到
的长(精确到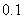 米)
米)
(参考数据: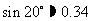 ,
,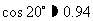 ,
,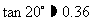 ,
,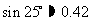 ,
,
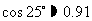 ,
,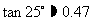 .)
.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com