
2.要使分式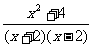 有意义,满足的条件是
有意义,满足的条件是
A.x≠O B.x≠2 C.x≠2且x≠一2 D.x≠2或x≠一2
1.有理式①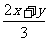 ; ②
; ②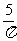 ; ③
; ③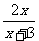 ; ④
; ④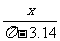 中是分式的是
中是分式的是
A.①② B.②③④ C.③ D.②④
28.(12分)已知m,n是方程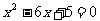 的两个实数根,且m<n.抛物线
的两个实数根,且m<n.抛物线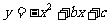 的图象经过点A(m,0),B(0,n).
的图象经过点A(m,0),B(0,n).
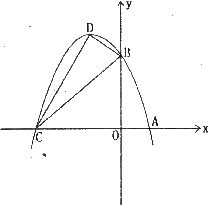
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一个交点为C,抛物线的顶点D.
试求出C、D的坐标和△BCD的面积.
(3)P是线段OC上的一点,过点P作PH⊥x轴与抛物线交于H点,若直线BC把APCH分成面积之比为2:3的两部分,请求出P点的坐标.
27.(10分)在2006年青岛崂山樱桃节前夕某果品批发公司为指导今年的樱桃销售,对往年的市场销售情况进了调查,统计得到如下数据:
|
销售价x(元/千克) |
… |
25 |
24 |
23 |
22 |
… |
|
销售量y(千克) |
… |
2000 |
2500 |
3000 |
3500 |
… |
(1)根据以上信息求出y与x之间的函数关系.
(2)若樱桃进价为13元/千克,试求销售利润P(元)与销售价x(元/千克)之间的函数关系,并求出当x为何值时,P的值最大?
26.(10分)如图AB、AC分别是⊙O的直径和弦,点D为劣弧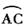 上的一点,弦ED分别交⊙O于点E,交AB于点H,交AC于点F,过C点的切线交ED的延长线于点P.
上的一点,弦ED分别交⊙O于点E,交AB于点H,交AC于点F,过C点的切线交ED的延长线于点P.
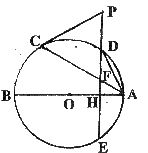
(1)若PC=PF,求证:AB⊥ED
(2)点D在劣弧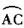 的什么位置时,才能使
的什么位置时,才能使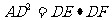 为什么?
为什么?
25.(8分)如图矩形ABCD的对角线AC、BD相交于点O、E、F分别是OA、OB的中点.
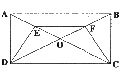
(1)求证:△ADE≌△BCF
(2)若AD=4cm,AB=8cm.求CF的长
24.(8分)有两个可以自由转动的均匀转盘A、B分别被分成4等份、3等份,如图所示,小伟和小强同学用这个转盘做游戏,游戏规则如下:
①分别转动转盘A和B.
②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止)
③如果和为0小伟获胜,否则小强获胜.
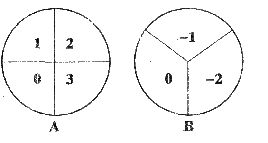
(1)用列表或树状图求小伟获胜的概率;
(2)你认为这个游戏对双方公平吗?请说明理由
23.(12分)求值:
(1)计算:
(2)求代数式的值。已知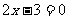 .
.
求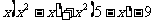 的值
的值
(3)课堂上李老师给大家出了这样一道题,当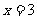 ,
,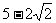 ,
,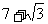 时,求代数式
时,求代数式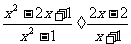 的值.小明一看“太复杂了怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
的值.小明一看“太复杂了怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
20.已知抛物线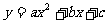 经过点A(一2,7),B(6,7),C(3,一8)则该抛物线上纵坐标为一8的另一点的坐标是 .
经过点A(一2,7),B(6,7),C(3,一8)则该抛物线上纵坐标为一8的另一点的坐标是 .
19.⊙O到直线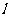 的距离为d,⊙O的半径为R,若d、R是方程
的距离为d,⊙O的半径为R,若d、R是方程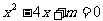 的两根,且直线
的两根,且直线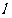 与⊙O相切,则m= .
与⊙O相切,则m= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com