
3.2007年3月27日,北京奥组委发布了北京2008年奥运会奖牌式样。请你为下面介绍奖牌的句子进行排序。(2分)
①奖牌背面镶嵌玉壁
②即站立的胜利女神和希腊潘纳辛纳科竞技场全景
③奖牌正面使用国际奥委会统一规定的图案
④奖牌的挂钩由中国传统玉双龙蒲纹璜演变而成
⑤玉壁正中的金属图形上镌刻着北京奥运会的会徽
2.文学常识填空。(3分)
(1)《史记》是我国第一部______________________;鲁迅用“___________________________,______________________________”高度评价了这部巨著的价值。
(2)宋词“豪放派”的代表人物主要是______________________________和辛弃疾,“婉约派”的代表人物是柳永和______________________________。
(3)《捕蛇者说》中的“说”是一种______________________________。
1.下列各组词语中各有一个错别字,请将改正后的字填写在括号里。(2分)
A.煦暖 相形见拙 拮据 阔绰 ( )
B.恻隐 无遐顾及 逶迤 脊梁 ( )
C.潮汛 不屑置辨 魁梧 祈愿 ( )
D.不言而谕 肇事 鉴赏 炫耀 ( )
26.如图,已知点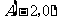 ,直线
,直线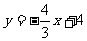 交
交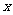 轴于点
轴于点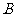 ,交
,交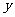 轴于点
轴于点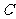
(1)求对称轴平行于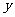 轴,且过
轴,且过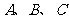 三点的抛物线解析式;
三点的抛物线解析式;
(2)若直线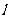 平分∠ABC,求直线
平分∠ABC,求直线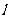 的解析式;
的解析式;
(3)若直线产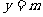 (
(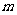 >0)交(1)中抛物线于
>0)交(1)中抛物线于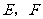 两点,问:
两点,问: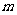 为何值时,以
为何值时,以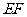 为边的正方形的面积为9?
为边的正方形的面积为9?

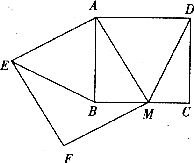
25.在正方形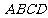 中,
中,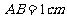 ,点
,点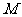 是
是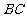 (端点除外)上一个动点,以
(端点除外)上一个动点,以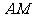 为边作正方形
为边作正方形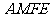 ,连接
,连接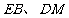 。
。
(1)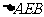 的面积是否变化?若不变化,请求出其面积;若变化,请说明理由。
的面积是否变化?若不变化,请求出其面积;若变化,请说明理由。
(2)探究: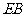 与
与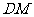 的关系。
的关系。
(3)点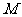 在何处时四边形
在何处时四边形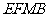 的面积最小?最小值是多少?
的面积最小?最小值是多少?
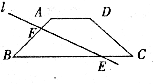
24.在等腰梯形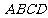 中,
中,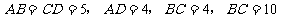 ,一条直线
,一条直线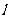 与下底
与下底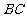 相交于点
相交于点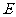 ,且直线
,且直线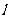 将等腰梯形
将等腰梯形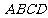 的周长平分。
的周长平分。
(1)如图,若直线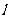 与腰
与腰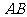 相交于点
相交于点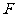 ,设
,设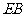 为
为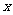 ,试用含
,试用含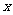 的代数式表示
的代数式表示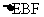 的面积;
的面积;
(2)是否存在直线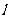 将等腰梯形
将等腰梯形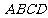 的周长和面积同时平分?若存在,指出符合要求的所有直线的特征;若不存在,请说明理由。
的周长和面积同时平分?若存在,指出符合要求的所有直线的特征;若不存在,请说明理由。
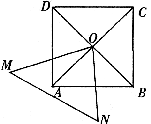
23.如图,边长为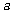 的正方形
的正方形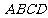 的中心为
的中心为 ,
,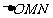 中,
中,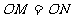 ,且
,且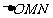 绕点
绕点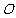 旋转时,能依次覆盖正方形各顶点(即各顶点在
旋转时,能依次覆盖正方形各顶点(即各顶点在 内)。
内)。
(1)当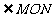 为多少度时,
为多少度时,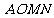 覆盖的正方形部分的面积始终为正方形面积的
覆盖的正方形部分的面积始终为正方形面积的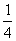 ?并说明理由;
?并说明理由;
(2)求满足(1)的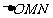 的面积的最小值;
的面积的最小值;
(3)若将条件中正方形换成正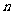 边形,其他条件不变,那么
边形,其他条件不变,那么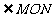 为多少度时,
为多少度时,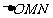 覆盖的正
覆盖的正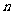 边形的面积始终为正
边形的面积始终为正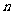 边形的
边形的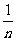 ?这样的
?这样的 的面积最小值为多少?(要求:只写出结果,不写解答过程)
的面积最小值为多少?(要求:只写出结果,不写解答过程)
22.某公司经营某种电子琴和洗衣机,市场需求量较大,每销售出一台电子琴,公司用于劳动力的投入500元,用于其他方面成本投入3000元,每销售出一台洗衣机,公司用于劳动力的投入1000元,用其他方面成本投入2000元。某月公司计划供应这两种产品12台。且用于劳动力的投入不超过1.1万元,用于其他方面成本投入不超过3万元。
(1)请你根据要求,设计出该月电子琴和洗衣机的供应方案;
(2)若每销售出一台电子琴和洗衣机公司获得的利润分别为600元和800元,则该月公司选择(1)中哪个方案可获得最大利润,最大利润是多少?
21.受台风的影响,一电线杆向西北方向倾斜了,初四·三班的数学小组要测一下此电线杆地上部分的长度。他们在电线杆的影子恰好指向西北方向时,测得电线杆的影子长11.19米,电线杆与影子的夹角为60°。又知此时地面竖立的2米长的木杆的影子长1米,请你计算一下电线杆地上部分的长度(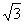 取1.73)。
取1.73)。
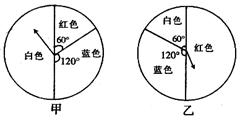
20.李明、张欣、杨武三同学都想参加学校组织的周末社会活动,而又只能参加一人,三位同学采用了两个转盘定人选的方法:
如图,规定同时转动甲乙两个转盘,两指针指向同一色为准(若指针指向分界线或不同色,重转),每人选一色,先转出的胜出。
三位同学思考片刻后,杨武选了蓝色,李明选了红色,而张欣选了白色。
你认为三同学胜出的机会相同吗?若不同,请说明哪位同学胜出的可能性较大;若机会相同,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com