
26.(本小题满分7分)
学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表:
|
一等奖 |
二等奖 |
三等奖 |
|
1盒福娃和1枚徽章 |
1盒福娃 |
1枚徽章 |
用于购买奖品的总费用不少于1000元但不超过1100元,小明在购买“福娃”和微章前,了解到如下信息:
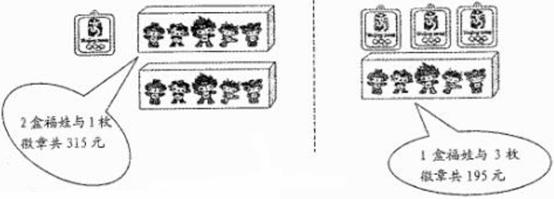
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
25.(本小题满分7分)
已知⊙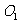 经过
经过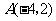 ,
,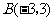 ,
,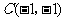 ,
,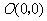 四点,一次函数
四点,一次函数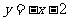 的图象是直线
的图象是直线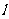 ,直线
,直线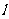 与
与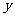 轴交于点
轴交于点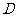 .
.
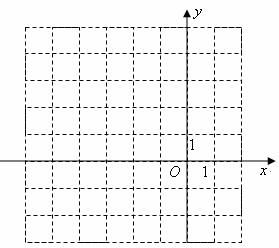
(1)在下面的平面直角坐标系中画出⊙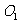 ,直线
,直线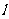 与⊙
与⊙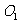 的交点坐标为
;
的交点坐标为
;
(2)若⊙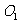 上存在整点
上存在整点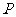 (横坐标与纵坐标均为整数的点称为整点),使得
(横坐标与纵坐标均为整数的点称为整点),使得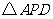 为等腰三角形,所有满足条件的点
为等腰三角形,所有满足条件的点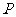 坐标为 ;
坐标为 ;
(3)将⊙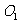 沿
沿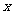 轴向右平移
个单位时,⊙
轴向右平移
个单位时,⊙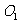 与
与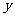 相切.
相切.
24.(本小题满分6分)
如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.
(1)设菱形相邻两个内角的度数分别为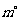 和
和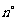 ,将菱形的“接近度”定义为
,将菱形的“接近度”定义为 ,于是,
,于是, 越小,菱形越接近于正方形.
越小,菱形越接近于正方形.
①若菱形的一个内角为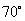 ,则该菱形的“接近度”等于
;
,则该菱形的“接近度”等于
;
②当菱形的“接近度”等于 时,菱形是正方形.
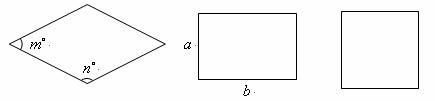
(2)设矩形相邻两条边长分别是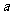 和
和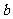 (
(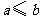 ),将矩形的“接近度”定义为
),将矩形的“接近度”定义为 ,于是
,于是 越小,矩形越接近于正方形.
越小,矩形越接近于正方形.
你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.
23.(本小题满分8分)
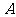 口袋中装有2个小球,它们分别标有数字
口袋中装有2个小球,它们分别标有数字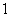 和
和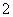 ;
;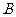 口袋中装有3个小球,它们分别标有数字
口袋中装有3个小球,它们分别标有数字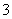 ,
,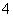 和
和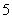 .每个小球除数字外都相同.甲、乙两人玩游戏,从
.每个小球除数字外都相同.甲、乙两人玩游戏,从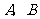 两个口袋中随机地各取出1个小球,若两个小球上的数字之和为偶数,则甲赢;若和为奇数,则乙赢.这个游戏对甲、乙双方公平吗?请说明理由.
两个口袋中随机地各取出1个小球,若两个小球上的数字之和为偶数,则甲赢;若和为奇数,则乙赢.这个游戏对甲、乙双方公平吗?请说明理由.
22.(本小题满分7分)
图1是某市2007年2月5日至14日每天最低气温的折线统计图.
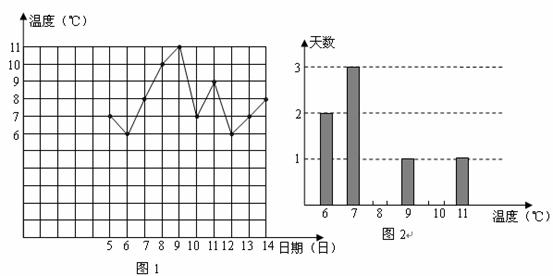
(1)图2是该市2007年2月5日至14日每天最高气温的频数分布直方图,根据图1提供的信息,补全图2中频数分布直方图;
(2)在这10天中,最低气温的众数是 ,中位数是 ,方差是 .
21.(本小题满分7分)
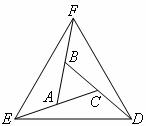
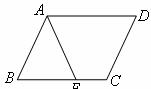
已知,如图,延长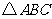 的各边,使得
的各边,使得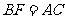 ,
,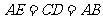 ,顺次连接
,顺次连接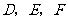 ,得到
,得到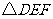 为等边三角形.
为等边三角形.
求证:(1)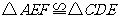 ;
;
(2)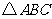 为等边三角形.
为等边三角形.
20.(本小题满分5分)
已知,如图,在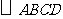 中,
中,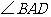 的平分线交
的平分线交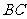 边于点
边于点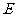 .
.
求证: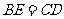 .
.
19.(本小题满分8分)解方程:
(1)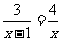 ;
(2)
;
(2)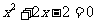 .
.
18.(本小题满分10分)化简:
(1)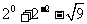 ;
(2)
;
(2)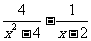 .
.
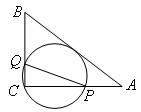
17.如图,在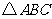 中,
中,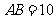 ,
,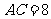 ,
,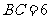 ,经过点
,经过点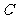 且与边
且与边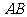 相切的动圆与
相切的动圆与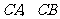 分别相交于点
分别相交于点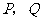 ,则线段
,则线段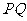 长度的最小值是( )
长度的最小值是( )
A.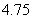 B.
B.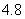 C.
C.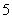 D.
D.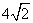
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com