
3.如图,已知△ABC为直角三角形,∠C =90°,若沿图中虚线剪去∠C,则∠1+∠2等于
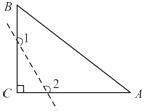
A.315° B.270° C.180° D.135°
2.下图是北京奥运会自行车比赛项目标志,图中两车轮所在圆的位置关系是

A.内含 B.相交 C.相切 D.外离
1.下列运算中,正确的是
A.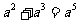 B.
B.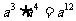
C.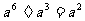 D.
D.
28.(本题满分12分)
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ,数量关系为 .
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
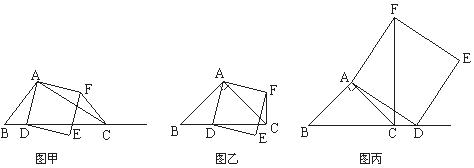
(2)如果AB≠AC,∠BAC≠90º,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若AC=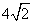 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
27.(本题满分12分)
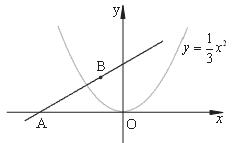
如图,直线 经过点B(
经过点B(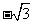 ,2),且与x轴交于点A.将抛物线
,2),且与x轴交于点A.将抛物线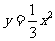 沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
(1)求∠BAO的度数;
(2)抛物线C与y轴交于点E,与直线AB交于两点,其中一个交点为F.
当线段EF∥x轴时,求平移后的抛物线C对应的函数关系式;
(3)在抛物线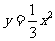 平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
25.(本题满分12分)
在购买某场足球赛门票时,设购买门票数为x(张),总费用为y(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
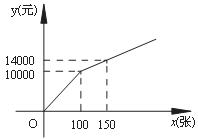
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中,y与x的函数关系式为 ;
方案二中,当0≤x≤100时,y与x的函数关系式为 ,
当x>100时,y与x的函数关系式为 ;
(2)如果购买本场足球赛门票超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
24.(本题满分10分)
一只不透明的袋子中装有4个小球,分别标有数字2、3、4、x,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
|
摸球总次数 |
10 |
20 |
30 |
60 |
90 |
120 |
180 |
240 |
330 |
450 |
|
“和为7”出现的频数 |
1 |
9 |
14 |
24 |
26 |
37 |
58 |
82 |
109 |
150 |
|
“和为7”出现的频率 |
0.10 |
0.45 |
0.47 |
0.40 |
0.29 |
0.31 |
0.32 |
0.34 |
0.33 |
0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为7”的频率将稳定在它的概
率附近.试估计出现“和为7”的概率;
(2)根据(1),若x是不等于2、3、4的自然数,试求x的值.
23.(本题满分8分)
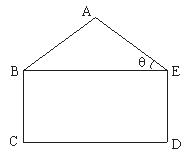
某工厂接受一批支援四川省汶川灾区抗震救灾帐蓬的生产任务.根据要求,帐篷的一个横截面框架由等腰三角形和矩形组成(如图所示).已知等腰△ABE的底角∠AEB=θ,且tanθ=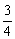 ,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
,矩形BCDE的边CD=2BC,这个横截面框架(包括BE)所用的钢管总长为15m.求帐篷的篷顶A到底部CD的距离.(结果精确到0.1m)
22.(本题满分8分)
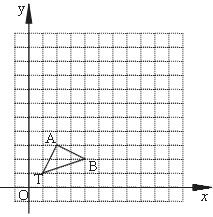
如图,在12×12的正方形网格中,△TAB 的顶点坐标分别为T(1,1)、A(2,3)、B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com