
25.(本小题满分10分)
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数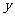 (亩)与补贴数额
(亩)与补贴数额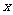 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系.随着补贴数额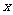 的不断增大,出口量也不断增加,但每亩蔬菜的收益
的不断增大,出口量也不断增加,但每亩蔬菜的收益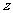 (元)会相应降低,且
(元)会相应降低,且 与
与 之间也大致满足如图2所示的一次函数关系.
之间也大致满足如图2所示的一次函数关系.
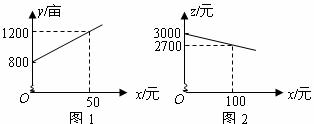
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数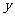 和每亩蔬菜的收益
和每亩蔬菜的收益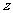 与政府补贴数额
与政府补贴数额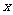 之间的函数关系式;
之间的函数关系式;
(3)要使全市这种蔬菜的总收益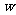 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额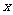 定为多少?并求出总收益
定为多少?并求出总收益 的最大值.
的最大值.
24.(本小题满分10分)
如图所示,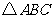 是直角三角形,
是直角三角形,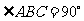 ,以
,以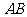 为直径的⊙O交
为直径的⊙O交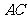 于点
于点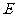 ,点
,点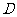 是
是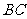 边的中点,连结
边的中点,连结 .
.
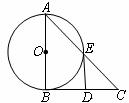
(1)求证: 与⊙O相切;
与⊙O相切;
(2)若⊙O的半径为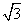 ,
,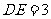 ,求
,求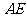 .
.
23.(本小题满分9分)
某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8∶20~12∶00,下午14∶00~16∶00,每天25元;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品件数与所用时间之间的关系见下表:
|
生产甲产品件数(件) |
生产乙产品件数(件) |
所用总时间(分) |
|
10 |
10 |
350 |
|
30 |
20 |
850 |
信息三:按件计酬,每生产一件甲产品可得1.50元,每生产一件乙产品可得2.80元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
22.(本小题满分9分)
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,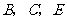 在同一条直线上,连结
在同一条直线上,连结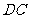 .
.
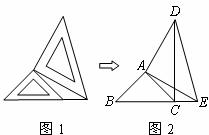
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明: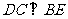 .
.
21.(本小题满分7分)
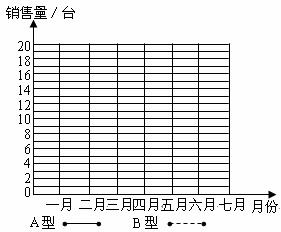
为了解某品牌A,B两种型号冰箱的销售状况,王明对其专卖店开业以来连续七个月的销售情况进行了统计,并将得到的数据制成如下的统计表:
|
月份 |
一月 |
二月 |
三月 |
四月 |
五月 |
六月 |
七月 |
|
A型销售量(单位:台) |
10 |
14 |
17 |
16 |
13 |
14 |
14 |
|
B型销售量(单位:台) |
6 |
10 |
14 |
15 |
16 |
17 |
20 |
(1)完成下表(结果精确到0.1):
|
|
平均数 |
中位数 |
方差 |
|
A型销售量 |
|
14 |
|
|
B型销售量 |
14 |
|
18.6 |
(2)请你根据七个月的销售情况在图中绘制成折线统计图,并依据折线图的变化趋势,对专卖店今后的进货情况提出建议(字数控制在20~50字).
20.(本小题满分8分)
(1)先化简,再求值: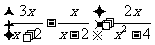 ,其中
,其中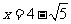 .
.
(2)用配方法解方程: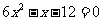 .
.
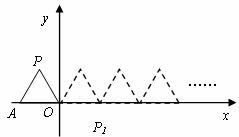
19.如图,将边长为1的正三角形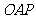 沿
沿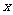 轴正方向连续翻转2008次,点
轴正方向连续翻转2008次,点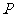 依次落在点
依次落在点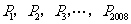 的位置,则点
的位置,则点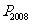 的横坐标为 .
的横坐标为 .
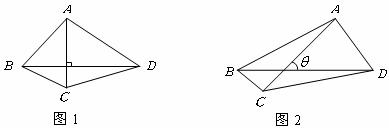
18.四边形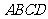 的对角线
的对角线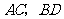 的长分别为
的长分别为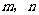 ,可以证明当
,可以证明当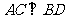 时(如图1),四边形
时(如图1),四边形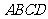 的面积
的面积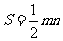 ,那么当
,那么当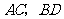 所夹的锐角为
所夹的锐角为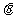 时(如图2),四边形
时(如图2),四边形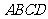 的面积
的面积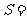 .(用含
.(用含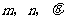 的式子表示)
的式子表示)
17.若等腰梯形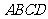 的上、下底之和为4,并且两条对角线所夹锐角为
的上、下底之和为4,并且两条对角线所夹锐角为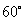 ,则该等腰梯形的面积为
(结果保留根号的形式).
,则该等腰梯形的面积为
(结果保留根号的形式).
16.不等式组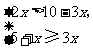 的解集为
.
的解集为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com