
7.在反比例函数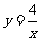 的图象中,阴影部分的面积不等于4的是( )
的图象中,阴影部分的面积不等于4的是( )
6.如图,已知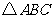 中,
中, ,
,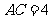 ,
,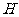 是高
是高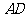 和
和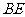 的交点,则线段
的交点,则线段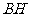 的长度为( )
的长度为( )
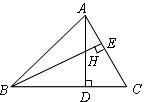
A.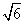 B.4 C.
B.4 C.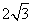 D.5
D.5
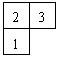
5.如图是由几个小立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,那么这个几何体的主视图是( )
4.不等式组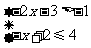 的解集在数轴上可表示为(
)
的解集在数轴上可表示为(
)
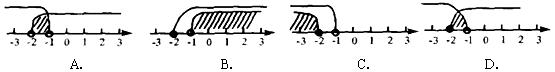
3.数据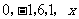 的众数为
的众数为 ,则这组数据的方差是(
)
,则这组数据的方差是(
)
A.2 B.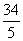 C.
C.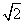 D.
D.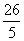
2.已知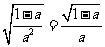 ,则
,则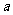 的取值范围是(
)
的取值范围是(
)
A.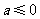 B.
B.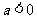 C.
C.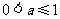 D.
D.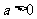
1.下列计算正确的是( )
A.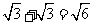 B.
B.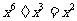
C.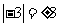 D.
D.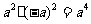
28.(本小题满分10分)
如图,在平面直角坐标系中,点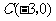 ,点
,点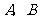 分别在
分别在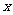 轴,
轴,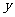 轴的正半轴上,且满足
轴的正半轴上,且满足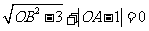 .
.
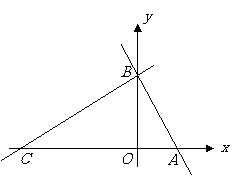

(1)求点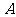 ,点
,点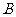 的坐标.
的坐标.
(2)若点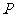 从
从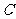 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线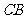 运动,连结
运动,连结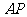 .设
.设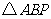 的面积为
的面积为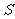 ,点
,点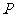 的运动时间为
的运动时间为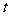 秒,求
秒,求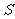 与
与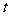 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点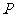 ,使以点
,使以点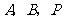 为顶点的三角形与
为顶点的三角形与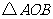 相似?若存在,请直接写出点
相似?若存在,请直接写出点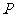 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
27.(本小题满分10分)
某工厂计划为震区生产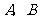 两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套
两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套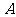 型桌椅(一桌两椅)需木料
型桌椅(一桌两椅)需木料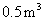 ,一套
,一套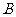 型桌椅(一桌三椅)需木料
型桌椅(一桌三椅)需木料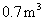 ,工厂现有库存木料
,工厂现有库存木料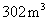 .
.
(1)有多少种生产方案?
(2)现要把生产的全部桌椅运往震区,已知每套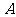 型桌椅的生产成本为100元,运费2元;每套
型桌椅的生产成本为100元,运费2元;每套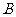 型桌椅的生产成本为120元,运费4元,求总费用
型桌椅的生产成本为120元,运费4元,求总费用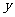 (元)与生产
(元)与生产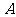 型桌椅
型桌椅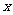 (套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用
(套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用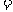 生产成本
生产成本 运费)
运费)
(3)按(2)的方案计算,有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由.
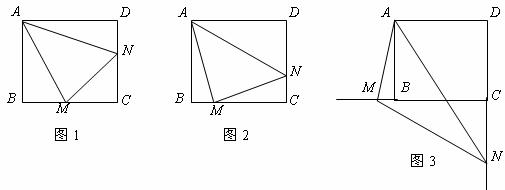
26.(本小题满分8分)
已知:正方形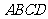 中,
中,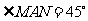 ,
,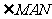 绕点
绕点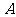 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交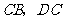 (或它们的延长线)于点
(或它们的延长线)于点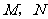 .
.
当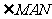 绕点
绕点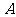 旋转到
旋转到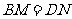 时(如图1),易证
时(如图1),易证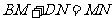 .
.
(1)当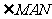 绕点
绕点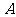 旋转到
旋转到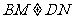 时(如图2),线段
时(如图2),线段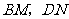 和
和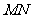 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当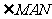 绕点
绕点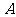 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段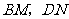 和
和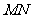 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com