
24.(本题满分12分)
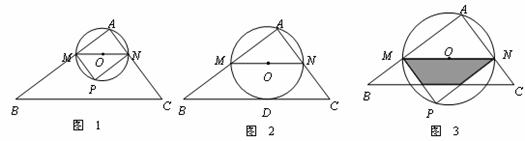
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
23.(本题满分10分)
(1)探究新知:
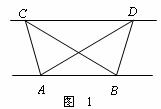
如下图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
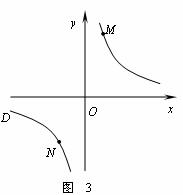
① 如下图2,点M,N在反比例函数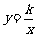 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
试证明:MN∥EF.
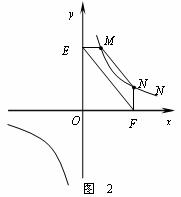
② 若①中的其他条件不变,只改变点M,N 的位置如图3所示,请判断 MN与EF是否平行.
22. (本题满分10分)
如下图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东45°方向、点B的北偏东30°方向上,AB=2km,∠DAC=15°.
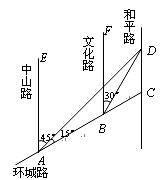
(1)求B,D之间的距离;
(2)求C,D之间的距离.
21.(本题满分9分)
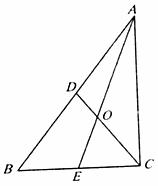
在Rt△ABC中,∠ACB=90°,中线AE与中线CD交于点O,AB=6.
(1)求证:AO︰OE=2︰1;
(2)求OC的长.
20.(本题满分9分)
某市2007年秋季开始,减免学生在义务教育阶段的学杂费,并按照每学期小学每生250元,初中每生450元的标准,由财政拨付学校作为办公经费,该十一学校小学生和初中生共有840人,2007年秋季收到当学期该项拨款290000元,该学校小学生和初中生各有多少人?
19.(本题满分8分)
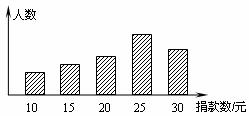
振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3︰4︰5︰8︰6,又知此次调查中捐款25元和30元的学生一共42人.
(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元?
18.(本题满分6分)
先化简,再求值:
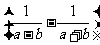 ÷
÷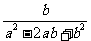 ,其中
,其中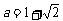 ,
,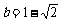 .
.
17.“上升数”是一个数中右边数字比左边数字大的自然数(如:34,568,2469等).任取一个两位数,是 “上升数”的概率是 .
16.将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:
|
所剪次数 |
1 |
2 |
3 |
4 |
… |
n |
|
正三角形个数 |
4 |
7 |
10 |
13 |
… |
an |
则an= (用含n的代数式表示).
15.分解因式: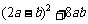 =____________.
=____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com