
1.4的平方根是_____________.
例6.方程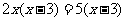 的根是( )
的根是( )
A.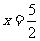 B.
B.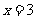 C.
C.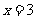 或
或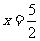 D.
D.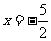
错解:方程两边同除以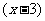 ,得
,得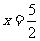 .选A.
.选A.
剖析:错解中,方程两边同除以因式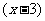 ,忽视了因式
,忽视了因式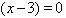 的情况,不属于同解变形,违背了等式的性质,造成漏解.因为方程
的情况,不属于同解变形,违背了等式的性质,造成漏解.因为方程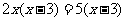 是一元二次方程,因此若有解,则有两个解.因此正确答案选C.
是一元二次方程,因此若有解,则有两个解.因此正确答案选C.
相信同学们会结合以上错解剖析,“对症下药”在自己解决与一元二次方程有关的问题时,避免这些错误的发生,更好的正确的解题.
例5.已知关于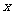 的方程
的方程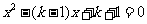 的两个实数根的平方和等于
的两个实数根的平方和等于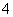 ,求实数
,求实数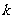 的值.
的值.
错解:设方程的两根为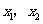 ,由根与系数的关系得,
,由根与系数的关系得,
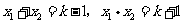 .又
.又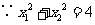 ,即
,即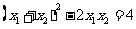 ,
∴
,
∴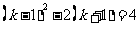 ,即
,即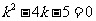 , ∴
, ∴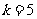 且
且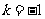 .
.
剖析:一元二次方程的根与系数的关系是以判别式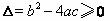 为前提,才能确保一元二次方程有两个实数根.错解中忽略了原方程有两根的条件
为前提,才能确保一元二次方程有两个实数根.错解中忽略了原方程有两根的条件 ,未将求出的
,未将求出的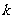 的值代入判别式中检验而造成错误.当
的值代入判别式中检验而造成错误.当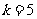 时,
时,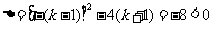 ,不符合题意舍去.当
,不符合题意舍去.当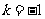 时
时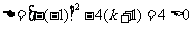 ,∴
,∴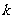 的值为
的值为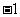 .因此要注意,要由
.因此要注意,要由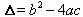 来判断一元二次方程的解.
来判断一元二次方程的解.
例4.已知关于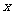 的方程
的方程 有两个不相等的实数根,求
有两个不相等的实数根,求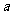 的取值范围.
的取值范围.
错解:∵关于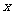 的方程
的方程 有两个不相等的实数根,∴
有两个不相等的实数根,∴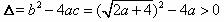 ,得
,得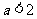 .
.
诊治:此题注意到信息“关于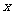 的方程
的方程 有两个不相等的实数根”,进而直接得到
有两个不相等的实数根”,进而直接得到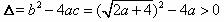 ,得
,得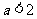 ;但却忽视了隐含条件二次根式
;但却忽视了隐含条件二次根式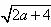 的被开方数
的被开方数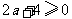 是非负数,即
是非负数,即 ,故而出错.所以
,故而出错.所以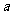 的取值范围是
的取值范围是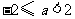 .因此,再解一元二次方程有关问题时,特别注意的判别式
.因此,再解一元二次方程有关问题时,特别注意的判别式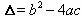 的确定.
的确定.
例3.已知关于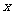 的方程
的方程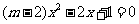 有解,那么
有解,那么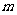 的取值范围是( )
的取值范围是( )
A.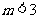 B.
B.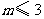 C.
C.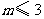 且
且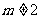 D.
D.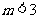 且
且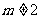
错解:由于方程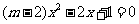 ,∴此方程为一元二次方程,故
,∴此方程为一元二次方程,故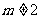 ,且
,且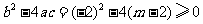 ,得
,得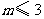 且
且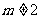 .
.
剖析:错解中忽视了“关于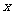 的方程
的方程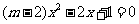 有解”中的关键词“关于
有解”中的关键词“关于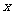 的方程”(未指明方程的类型);关键词“有解”(不能来判断该方程是一元二次方程).因此,此方程
的方程”(未指明方程的类型);关键词“有解”(不能来判断该方程是一元二次方程).因此,此方程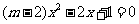 有两种可能:若方程为一元二次方程,则“有解”与“有两个实数根”是等同的,则
有两种可能:若方程为一元二次方程,则“有解”与“有两个实数根”是等同的,则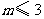 且
且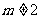 ;若方程为一元一次方程,则
;若方程为一元一次方程,则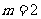 ,解得
,解得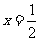 ,即解
,即解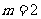 也符合题意.所以本题的正确答案是
也符合题意.所以本题的正确答案是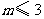 .因此要注意题中信息所包含的隐含条件.
.因此要注意题中信息所包含的隐含条件.
例2.已知关于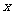 的方程
的方程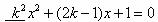 有两个不相等的实数根,求
有两个不相等的实数根,求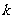 的取值范围.
的取值范围.
错解:根据题意,得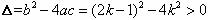 ,解得
,解得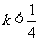 .∴当
.∴当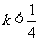 时,方程有两个不相等的实数根.
时,方程有两个不相等的实数根.
剖析:注意已知条件中的“关键词”方程有两个不相等的实数根,显然此方程必为一元二次方程,所以二次项系数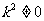 即
即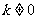 .因此错解中漏掉了
.因此错解中漏掉了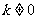 ,故而正确答案为
,故而正确答案为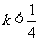 ,且
,且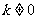 .因此解题要注意题中的关键词.
.因此解题要注意题中的关键词.
例1 用公式法解方程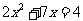 .
.
错解:
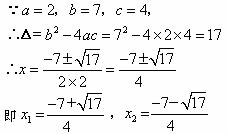
剖析:错解中没有将方程化成“一般形式”,造成系数中常数项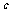 的错误.应该先移项得到
的错误.应该先移项得到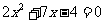 ,则
,则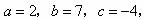
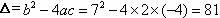 .进一步用求根公式:
.进一步用求根公式: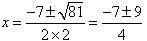 ,即
,即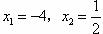 .
.
⑴ 若方程有两个相等的实数根,求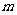 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)
⑵ 是否存在正数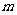 ,使方程的两个实数根的平方和等于224 ?若存在,求出满足条件的
,使方程的两个实数根的平方和等于224 ?若存在,求出满足条件的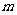 的值; 若不存在,请说明理由。(6分)
的值; 若不存在,请说明理由。(6分)
②当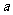 取什么值时,方程有两个相等的实数根?③当
取什么值时,方程有两个相等的实数根?③当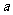 取什么值时,方程没有实数根?(9分)
取什么值时,方程没有实数根?(9分)
①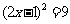 (直接开平方法)②
(直接开平方法)②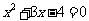 (用配方法)③
(用配方法)③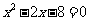 (用因式分解法)
(用因式分解法)
④.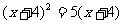 ⑤
⑤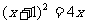 ⑥.
⑥.
⑦.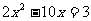 ⑧.x-2)(x-5)=-2
⑧.x-2)(x-5)=-2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com