
21.(12分)已知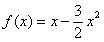 ,设0<
,设0<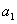 <
<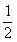 ,
,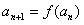
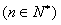 。用数学归纳法证明
。用数学归纳法证明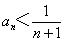
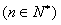
20.(12分)设函数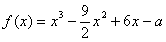
(1)对于任意实数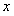 ,
,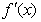 ≥
≥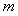 恒成立,求实数
恒成立,求实数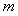 的最大值;
的最大值;
(2)若方程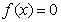 有且仅有一个实根,求实数
有且仅有一个实根,求实数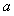 的取值范围。
的取值范围。
19.(12分)盒子中有大小相同的球10个,其中标号为1的球有3个,标号为2的球有4个,标号为5的球有3个。第一次从盒中任取一个球,放回后第二次再任取一个球(假设取到每个球的可能性都相同),记第一次与第二次取到球的标号之和为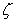 ,求
,求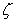 的概率分布列及数学期望
的概率分布列及数学期望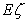 。
。
18.(12分)(理)设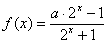 是
是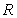 上的奇函数
上的奇函数
(1)求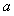 的值;
的值;
(2)求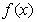 的反函数
的反函数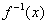 ;
;
(3)对任意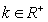 ,解关于
,解关于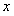 的不等式
的不等式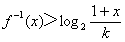 。
。
17.(10分)已知命题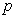 :
: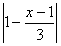 ≤2,命题
≤2,命题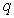 :
: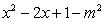 ≤0(
≤0(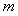 >0)
>0)
若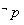 是
是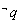 的必要不充分条件,求实数
的必要不充分条件,求实数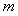 的取值范围。
的取值范围。
16.定义在R上的函数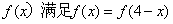 ,
,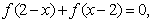
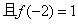 ,则
,则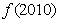 =____________。
=____________。
15.已知函数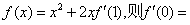 ____________。
____________。
14.若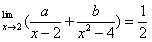 ,则
,则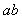 =____________。
=____________。
13.函数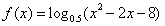 的单调递减区间是____________。
的单调递减区间是____________。
12.已知定义在R上的奇函数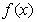 满足
满足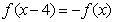 ,且在区间
,且在区间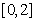 上是增函数。若方程
上是增函数。若方程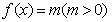 在区间
在区间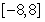 上有四个不同的实根
上有四个不同的实根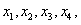 则
则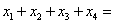 ( )
( )
A.8 B.4 C.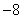 D.
D.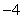
第Ⅱ卷(共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com