2．现今考古发掘出许多具有很高历史价值的青铜器如：司戊鼎，青铜编钟，四羊方尊，莲鹤方壶，下列有关青铜工艺的表述中正确的是

①青铜铸造是夏和商手工业的主要部门

②商周是我国历史上的“青铜时代”

③夏商的青铜业制品主要是满足国王和贵族使用

④周的青铜产品趋向生活化，日用器具数量增多

A．①②③④　　　　　　　 B．②③④　　　　　 C．②③④　　　　　 D．①③④

1、《孟子·告子》载：“诸候朝天子曰述职；……一不朝，则贬其爵；再不朝，则削其地；三不朝，则六师移之。”有关这段历史材料反映的制度表述不正确的是

A．天子与诸侯的关系是中央与地方的关系

B．世代诸侯需由中央任命，诸侯国拱卫中央

C．东周时期这项制度随井田制的瓦解而崩溃

D．这项制度下土地的所有者与使用者是分离的

4. 若棱长均相等的三棱锥叫正四面体，求棱长为a的正四面体的高.

3. 棱台的上、下底面积分别是25和81，高为4，求截得这棱台的原棱锥的高

2. 已知长方体的长、宽、高之比为4∶3∶12，对角线长为26cm, 则长、宽、高分别为多少？

1. 练习：书P7 　2 (2)题.

5. 小结：学习了柱、锥、台、球的定义、表示；性质；分类.

4. 练习：圆锥底面半径为1cm，高为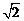cm，其中有一个内接正方体，求这个内接正方体的棱长. (补充平行线分线段成比例定理)

3. 教学简单组合体的结构特征：

① 讨论：矿泉水塑料瓶由哪些几何体构成？灯管呢？

② 定义：由柱、锥、台、球等几何结构特征组合的几何体叫简单组合体.

　 →列举生活中的实例

2．教学球体的结构特征：

① 定义：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体，叫球体.

→列举生活中的实例

结合图形认识：球心、半径、直径.

→ 球的表示.

② 讨论：球有一些什么几何性质？

③ 讨论：球与圆柱、圆锥、圆台有何关系？(旋转体)

棱台与棱柱、棱锥有什么共性？(多面体)