
2.在同一个平面上有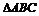 及一点O满足关系式:
及一点O满足关系式: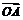 2+
2+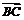 2=
2=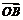 2+
2+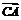 2=
2=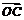 2+
2+
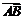 2,则O为△ABC的( D )
2,则O为△ABC的( D )
A.外心 B.内心 C.重心 D.垂心
1.已知A、B、C是平面上不共线的三点,O是三角形ABC的重心,动点P满足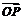 =(
=(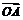 +
+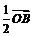 +2
+2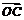 ),则点P一定为三角形ABC的( B)
),则点P一定为三角形ABC的( B)
A.AB边中线的中点 B.AB边中线的三等分点(非重心) C.重心 D.AB边的中点
分析:取AB边的中点M,则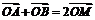 ,
,
由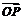 =(
=(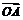 +
+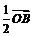 +2
+2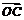 )可得3
)可得3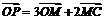 ,
,
∴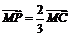 ,即点P为三角形中AB边上的中线的一个三等分点,且点P不过重心。
,即点P为三角形中AB边上的中线的一个三等分点,且点P不过重心。
6. 练习题
5.与三角形的“四心”有关的高考连接题及其应用
 例1:(2003年全国高考题)
例1:(2003年全国高考题)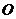 是平面上一定点,A、B、C是平面上不共线的三点,动点P满足
是平面上一定点,A、B、C是平面上不共线的三点,动点P满足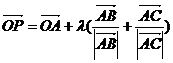 ,
,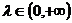 ,则动点P的轨迹一定通过△ABC的( )
,则动点P的轨迹一定通过△ABC的( )
(A)外心 (B)内心
(C)重心 (D)垂心
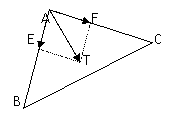
事实上如图设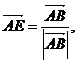
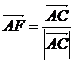 都是单位向量
都是单位向量
易知四边形AETF是菱形 故选答案B
例2:(2005年北京市东城区高三模拟题)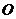 为△ABC所在平面内一点,如果
为△ABC所在平面内一点,如果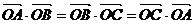 ,则O必为△ABC的( )
,则O必为△ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
事实上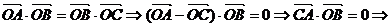 OB⊥CA
故选答案D
OB⊥CA
故选答案D
例3:已知O为三角形ABC所在平面内一点,且满足
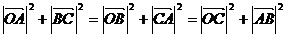 ,则点O是三角形ABC的( )
,则点O是三角形ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
事实上由条件可推出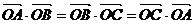 故选答案D
故选答案D
例4:设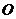 是平面上一定点,A、B、C是平面上不共线的三点,
是平面上一定点,A、B、C是平面上不共线的三点,
动点P满足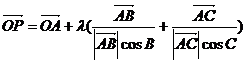 ,
,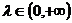 ,则动点P的轨迹一定通过△ABC的( )
,则动点P的轨迹一定通过△ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
事实上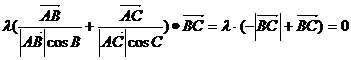 故选答案D
故选答案D
例5: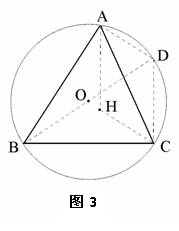 2005年全国(I)卷第15题“
2005年全国(I)卷第15题“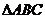 的外接圆的圆心为
的外接圆的圆心为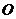 ,两条边上的高的交点为
,两条边上的高的交点为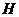 ,
,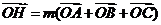 ,则实数
,则实数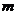 =________”
=________”
先解决该题:
作直经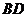 ,连
,连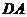 ,
,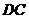 ,有
,有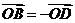 ,
,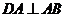 ,
,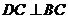 ,
,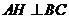 ,
,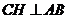 ,故
,故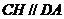 ,
,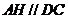
故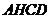 是平行四边形,进而
是平行四边形,进而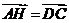 ,又
,又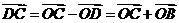
∴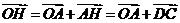
故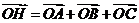 ,所以
,所以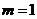
评注:外心的向量表示可以完善为:
若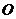 为
为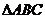 的外心,
的外心,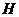 为垂心,则
为垂心,则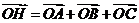 。其逆命题也成立。
。其逆命题也成立。
例6.已知向量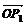 ,
,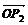 ,
,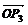 满足条件
满足条件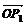 +
+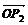 +
+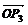 =0,|
=0,|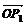 |=|
|=|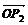 |=|
|=|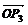 |=1,
|=1,
求证: △P1P2P3是正三角形.(《数学》第一册(下),复习参考题五B组第6题)
证明: 由已知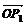 +
+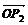 =-
=-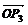 ,两边平方得
,两边平方得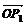 ·
·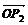 =
=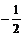 ,
,
同理 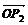 ·
·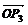 =
=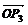 ·
·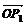 =
=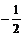 , ∴|
, ∴|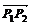 |=|
|=|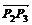 |=|
|=|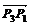 |=
|=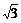 ,从而△P1P2P3是正三角形.
,从而△P1P2P3是正三角形.
反之,若点O是正三角形△P1P2P3的中心,则显然有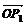 +
+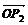 +
+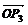 =0且|
=0且|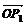 |=|
|=|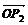 |=|
|=|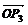 |,即O是△ABC所在平面内一点,
|,即O是△ABC所在平面内一点,
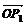 +
+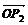 +
+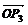 =0且|
=0且|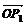 |=|
|=|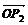 |=|
|=|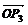 |
|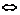 点O是正△P1P2P3的中心.
点O是正△P1P2P3的中心.
4. 欧拉线的4种证法
三角形的外心、重心、九点圆圆心、垂心,依次位于同一直线上,这条直线就叫三角形的欧拉线。
在△ABC中,已知O、G、H分别是三角形的外心、重心、垂心。求证:O、G、H三点共线,且OG:GH=1:2。(证九点园园心在欧拉线上略,可查有关资料)
欧拉线的证法1:(平面几何法)
关于欧拉线的介绍详见:欧拉线,下面是欧拉线的证明
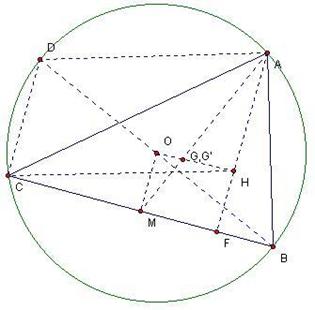
如图,H、G、O分别是△ABC的垂心、重心、外心, 连AH,作△ABC的外接圆直径BOD, 再连DC、DA,则DC⊥BC…①,DA⊥AB…② ∵H为△ABC垂心 ∴AH⊥BC…③,CH⊥AB…④ 由①、③可知DC∥AH,由②、④可知DA∥CH,故四边形ADCH为平行四边形,∴AH=DC。
∵点O与点M分别是BD、CB的中点 ∴DC=2OM,即AH=2OM。 作BC边上的中线AM,连OM、OH;设OH交AM与点G' ∵OM⊥BC,△AHG'∽△MOG',AH=DC=2OM, ∴AG'=2G'M,因此G'即△ABC重心G。 故△ABC的垂心H、重心G和外心O三点共线,直线HGO即欧拉线。
评注:利用垂心H、外心O作为已知,证中线AM与OH的交点G'为重心。
欧拉线的证法2:(平面几何法)
设H,G,O,分别为△ABC的垂心、重心、外心
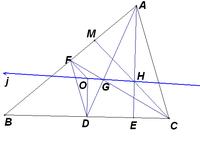
连接AG并延长交BC于D, 则可知D为BC中点。
连接OD ,又因为O为外心,所以OD⊥BC。连接AH并延长交BC于E,因H为垂心,所以 AE⊥BC。所以OD//AE,有∠ODA=∠EAD。由于G为重心,则GA:GD=2:1。
连接CG并延长交BA于F,则可知D为BC中点。同理,OF//CM.所以有
∠OFC=∠MCF
连接FD,有FD平行AC,且有DF:AC=1:2。FD平行AC,所以∠DFC=∠FCA,∠FDA=∠CAD,又∠OFC=∠MCF,∠ODA=∠EAD,相减可得∠OFD=∠HCA,∠ODF=∠EAC,所以有△OFD∽△HCA,所以OD:HA=DF:AC=1:2;又GA:GD=2:1所以HA: OD=GA:GD=2:1,又∠ODA=∠EAD,所以△OGD∽△HGA。所以∠OGD=∠AGH,,所以∠OGD +∠OGA=180°,所以∠AGH +∠OGA =180°。即O、G、H三点共线。
评注:利用重心G、外心O作为已知,证垂心H在直线OG上。
欧拉线的证法3:(向量法)
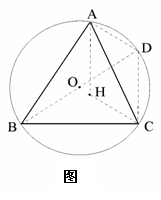 设H,G,O,分别为△ABC的垂心、重心、外心.
设H,G,O,分别为△ABC的垂心、重心、外心.
①若 为
为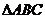 的外心,
的外心,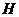 为垂心
为垂心
求证: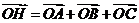 。
。
作直经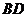 ,连
,连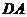 ,
,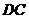 ,有
,有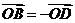 ,
,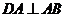 ,
,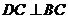 ,
,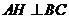 ,
,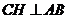 ,故
,故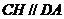 ,
,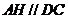 ,故
,故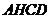 是平行四边形,
是平行四边形, 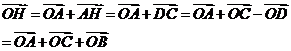
故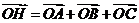
②若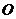 为
为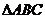 的外心,G为重心
的外心,G为重心
求证: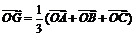
证明 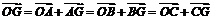
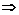
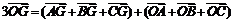
∵G是△ABC的重心
∴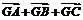 =
=
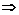
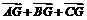 =
= ,即
,即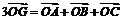
由此可得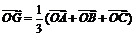 .(反之亦然(证略))
.(反之亦然(证略))
③由①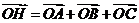 ,由②
,由②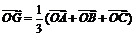
∴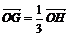 ,
,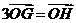
所以O、G、H三点共线.
欧拉线的证法4:(向量的坐标法)
在△ABC中,已知Q、G、H分别是三角形的外心、重心、垂心。求证:Q、G、H三点共线,且QG:GH=1:2。
[证明]:以A为原点,AB所在的直线为x轴,建立如图所示的直角坐标系。设A(0,0)、B(x1,0)、C(x2,y2),D、E、F分别为AB、BC、AC的中点,则有:
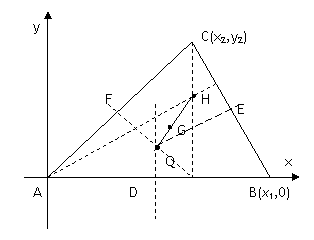
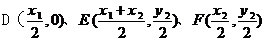
由题设可设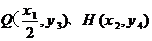 ,
,
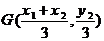 ,
,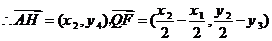
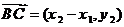
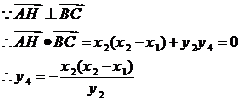
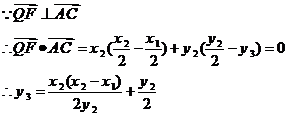
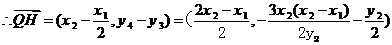
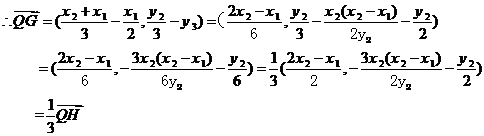
即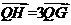 ,故Q、G、H三点共线,且QG:GH=1:2
,故Q、G、H三点共线,且QG:GH=1:2
[注]:本例用平面几何知识、向量的代数运算和几何运算处理,都较麻烦,而借用向量的坐标形式,将向量的运算完全化为代数运算,这样就将“形”和“数”紧密地结合在一起,从而,很多对称、共线、共点、垂直等问题的证明,都可转化为熟练的代数运算的论证。
3.与三角形的“四心”有关的一些常见的其它向量关系式
① 设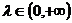 ,则向量
,则向量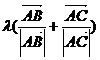 必平分∠BAC,该向量必通过△ABC的内心;
必平分∠BAC,该向量必通过△ABC的内心;
② 设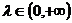 ,则向量
,则向量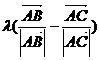 必平分∠BAC的邻补角
必平分∠BAC的邻补角
③ 设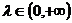 ,则向量
,则向量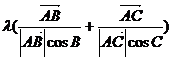 必垂直于边BC,该向量必通过△ABC的垂心
必垂直于边BC,该向量必通过△ABC的垂心
④ △ABC中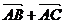 一定过
一定过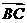 的中点,通过△ABC的重心
的中点,通过△ABC的重心
⑤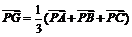
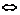
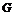 为△ABC的重心(P是平面上任意点).
为△ABC的重心(P是平面上任意点).
证明 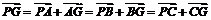
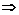
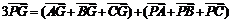
∵G是△ABC的重心
∴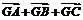 =
=
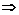
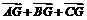 =
= ,即
,即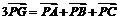
由此可得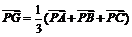 .(反之亦然(证略))
.(反之亦然(证略))
⑤ △ABC的外心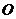 、重心
、重心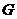 、垂心
、垂心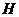 共线,即
共线,即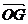 ∥
∥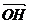
证明:(详细证明见欧拉线的证明)
按重心定理 G是△ABC的重心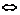
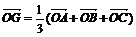
按垂心定理 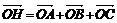 ,由此可得
,由此可得 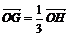 .
.
⑥ 设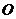 为△ABC所在平面内任意一点,I为△ABC的内心,
为△ABC所在平面内任意一点,I为△ABC的内心,
* 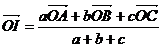

内心I(,)
证明:由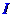 是
是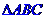 的内心
的内心
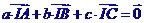 。(其中
。(其中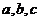 是
是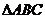 三边)(见内心的充要条件的证明)
三边)(见内心的充要条件的证明)
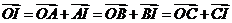
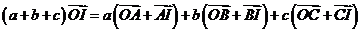
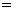
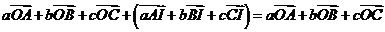
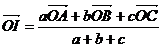 , ∴I(,).
, ∴I(,).
2. 三角形的“四心” 定理的平面向量表达式及其证明
三角形的“四心” 定理的平面向量表达式及其证明
① 是
是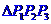 的重心
的重心
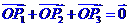 (其中
(其中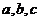 是
是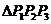 三边)
三边)
证明:充分性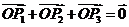
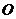 是
是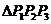 的重心
的重心
若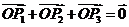 ,则
,则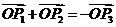 ,以
,以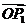 ,
,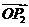 为邻边作平行四边形
为邻边作平行四边形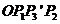 ,设
,设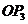 与
与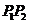 交于点
交于点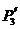 ,则
,则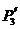 为
为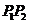 的中点,有
的中点,有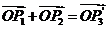 ,得
,得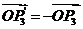 ,即
,即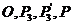 四点共线,故
四点共线,故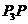 为
为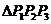 的中线,同理,
的中线,同理,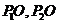 亦为
亦为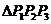 的中线,所以,
的中线,所以, 为的重心。
为的重心。
必要性: 是
是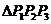 的重心
的重心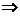
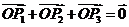
如图,延长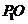 交
交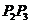 于
于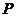 ,则
,则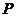 为
为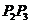 的中点,由重心的性质得
的中点,由重心的性质得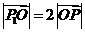 .
.
∵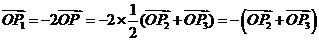 ∴
∴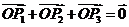
 ②点
②点 是
是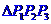 的垂心
的垂心
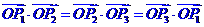
证明: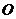 是
是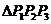 的垂心
的垂心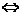
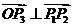 ,
,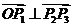
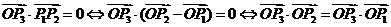 同理
同理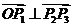
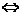
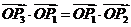
故当且仅当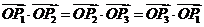 .
.
 ③点
③点 是
是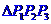 的外心
的外心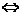
 .
.
证明:O是△ABC的外心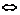 |
|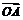 |=|
|=|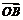 |=|
|=|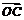 |(或
|(或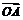 2=
2=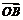 2=
2=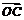 2)(点O到三边距离相等)
2)(点O到三边距离相等)
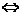 (
(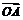 +
+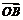 )·
)·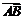 =(
=(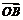 +
+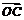 )·
)·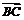 =(
=(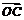 +
+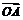 )·
)·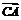 =0(O为三边垂直平分线的交点)
=0(O为三边垂直平分线的交点)
④ 是
是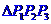 的内心
的内心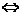
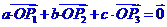 。(其中
。(其中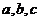 是
是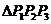 三边)
三边)
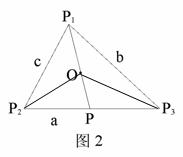 证明:充分性:
证明:充分性: 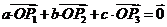
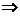
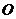 是
是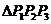 的内心
的内心
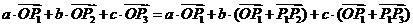 =
=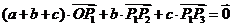
所以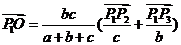 ,而
,而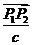 ,
,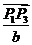 分别是
分别是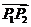 ,
,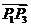 方向上的单位向量,所以向量
方向上的单位向量,所以向量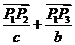 平分
平分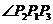 ,即
,即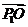 平分
平分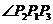 ,同理
,同理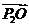 平分
平分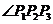 ,得到点
,得到点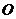 是
是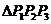 的内心。
的内心。
必要性: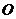 是
是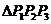 的内心
的内心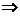
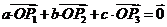
若点O为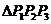 的内心,延长
的内心,延长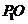 交
交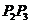 于
于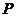 ,由三角形内角平分线的性质定理,有
,由三角形内角平分线的性质定理,有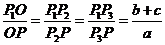 ,于是
,于是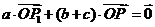
再由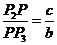 ,有
,有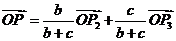 (定比分点)代入前式中便得
(定比分点)代入前式中便得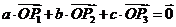 .
.
必要性证法二:设O是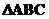 内任一点,以O为坐标原点,OA所在直线为x轴,建立直角坐标系。并设
内任一点,以O为坐标原点,OA所在直线为x轴,建立直角坐标系。并设
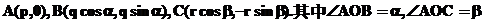
显然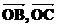 不共线,由平面向量基本定理,可设
不共线,由平面向量基本定理,可设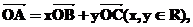 则
则
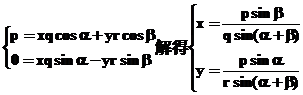
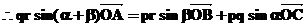
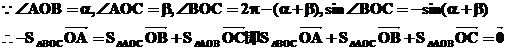
(ⅰ)若O是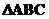 的内心,则
的内心,则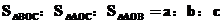
故 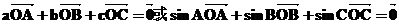
必要性得证.同时还可得到以下结论
(ⅱ)若O是 的重心,则
的重心,则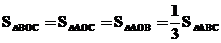
故
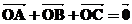
(ⅲ)若O是 的外心
的外心
则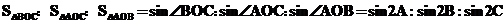
 故
故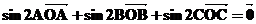
(ⅳ)若O是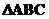 (非直角三角形)的垂心,
(非直角三角形)的垂心,
则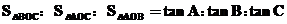
故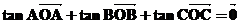
证明: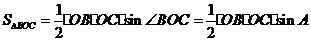
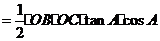 (A 、E、O 、F四点共圆)同理
(A 、E、O 、F四点共圆)同理
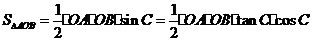
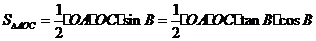
因此只需证
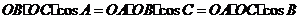
先证第一个等式
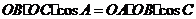
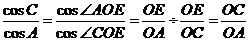 (E 、C、D、O四点共圆,
(E 、C、D、O四点共圆,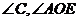 为
为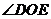 的补角;E 、O、F、A四点共圆,
的补角;E 、O、F、A四点共圆,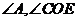 为
为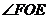 的补角)所以上式成立,即第一个等式成立。同理可证:该连等式成立,原题得证。
的补角)所以上式成立,即第一个等式成立。同理可证:该连等式成立,原题得证。
评注:一箭四雕,需要提醒的是,这里只探求了三角形内心向量形式的必要条件,充分性并未证明。
1.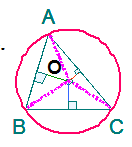 三角形的“四心”定理的平面几何证明
三角形的“四心”定理的平面几何证明
①三角形三边的中垂线交于一点,这一点为三角形外接圆的圆心,称外心。
证明: 设AB、BC的中垂线交于点O, 则有OA=OB=OC,
故O也在AC的中垂线上,因为O到三顶点的距离相等,
故点O是ΔABC外接圆的圆心. 因而称为外心.
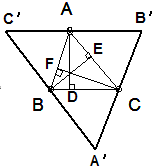 ②三角形三边上的高交于一点,这一点叫三角形的垂心。
②三角形三边上的高交于一点,这一点叫三角形的垂心。
证明: AD、BE、CF为ΔABC三条高,过点A、B、C分别作对边的平行线,相交成ΔA′B′C′,AD为B′C′的中垂线;同理BE、CF也分别为 A′C′、A′B′的中垂线, 由外心定理,它们交于一点,
命题得证.
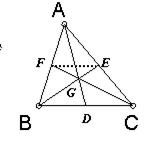 ③三角形三边中线交于一点,这一点叫三角形的重心。
③三角形三边中线交于一点,这一点叫三角形的重心。
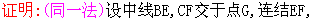
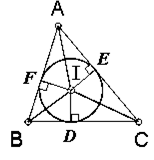 ④三角形三内角平分线交于一点,这一点为三角形内切圆的圆心,称内心。
④三角形三内角平分线交于一点,这一点为三角形内切圆的圆心,称内心。
证明 : 设∠A、∠C的平分线相交于I,
过I作ID⊥BC,IE⊥AC, IF⊥AB,则有IE=IF=ID.
因此I也在∠C的平分线上,即三角形三内角平分线交于一点.
17、 (10分)一个物体在斜面上以一定的速度沿斜面向上运动,斜面底边水平,斜面倾角θ可在0∽900间变化,设物体达到的最大位移x和倾角θ间的关系如图10所示,求物体与斜面间的动摩擦因数µ。
(10分)一个物体在斜面上以一定的速度沿斜面向上运动,斜面底边水平,斜面倾角θ可在0∽900间变化,设物体达到的最大位移x和倾角θ间的关系如图10所示,求物体与斜面间的动摩擦因数µ。
16、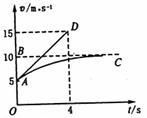 (12分)已知人和雪橇的总质量m=75kg,沿倾角
(12分)已知人和雪橇的总质量m=75kg,沿倾角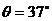 且足够长的斜坡向下滑动,滑动时雪橇所受的空气阻力
且足够长的斜坡向下滑动,滑动时雪橇所受的空气阻力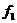 与速度
与速度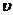 成正比,比例系数(即空气阻力系数)k未知。从某时刻开始计时,测得雪橇运动的
成正比,比例系数(即空气阻力系数)k未知。从某时刻开始计时,测得雪橇运动的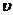 -t图线如图9中的曲线AC所示,图中BC是不行于Ot轴的直线,AD是过A点所作的曲线AC的切线,且A点的坐标为(0,5),D点的坐标为(4,15),由
-t图线如图9中的曲线AC所示,图中BC是不行于Ot轴的直线,AD是过A点所作的曲线AC的切线,且A点的坐标为(0,5),D点的坐标为(4,15),由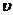 -t图的物理意义可知:
-t图的物理意义可知: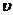 -t图线上每点所对应的物体运动的加速度在数值上等于通过该点切线的斜率。已知sin37°=0.60,cos37°=0.80,g取10m/s2。
-t图线上每点所对应的物体运动的加速度在数值上等于通过该点切线的斜率。已知sin37°=0.60,cos37°=0.80,g取10m/s2。
(1)试说明雪橇的运动情况。(先做什么运动?加速度的大小怎样变化?速度的大小怎样变化?后来做什么运动)
(2)当雪橇的速度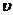 =5m/s时,它的加速度为多大?
=5m/s时,它的加速度为多大?
(3)求空气阻力系数k和雪橇与斜坡间的动摩擦因数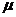 。 图9
。 图9
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com