
2.给出递推关系求通项,有时可以用归纳,猜想,证明的思路;而证明型的问题用数学归纳法往往是一种比较简单的方法;而给出铺垫(转化后的数列)的问题常常可以用证明(变换,待定系数法等)处理,一般难度不大。
例7:已知数 的递推关系为 ,且 求通项 。
解:∵ ∴ 令 则辅助数列 是公比为2的等比数列
∴ 即 ∴
例5. 在数列 中, , , ,求 。
解析:在 两边减去 ,得
∴ 是以 为首项,以 为公比的等比数列,∴ ,由累加法得
= = … = = =
例8: 已知数列{ }中 且 ( ),,求数列的通项公式。
解:∵ ∴ , 设 ,则
故{ }是以 为首项,1为公差的等差数列 ∴ ∴
点评:这种方法类似于换元法, 主要用于已知递推关系式求通项公式。
趣谈数列的通项问题及其思维方式
1.递推关系的形成:直接给出,函数给出,解析几何给出,应用问题给出,方程给出。
例6:设数列 的各项是一个等差数列与一个等比数列对应项的和,若c1=2,c2=4,c3=7,c4=12,求通项公式cn
解:设
例6. 已知数列 中, , ,
其中b是与n无关的常数,且 。求出用n和b表示的an的关系式。
解析:递推公式一定可表示为
的形式。由待定系数法知:
故数列 是首项为 ,公比为 的等比数列,故
点评:用待定系数法解题时,常先假定通项公式或前n项和公式为某一多项式,一般地,若数列 为等差数列:则 , (b、c为常数),若数列 为等比数列,则 , 。
例5:已知下列两数列 的前n项和sn的公式,求 的通项公式。(1) 。 (2)
解: (1) = = =3
此时, 。∴ =3 为所求数列的通项公式。
(2) ,当 时
由于 不适合于此等式 。 ∴
点评:要先分n=1和 两种情况分别进行运算,然后验证能否统一。
例4:在数列{ }中, =1, (n+1)· =n· ,求 的表达式。
解:由(n+1)· =n· 得 , = · · … = 所以
例4. 已知数列 中, ,前 项和 与 的关系是 ,试求通项公式 。
解析:首先由 易求的递推公式:
将上面n—1个等式相乘得:
点评:一般地,对于型如 = (n)· 类的通项公式,当 的值可以求得时,宜采用此方法。
例3:已知数列6,9,14,21,30,…求此数列的一个通项。
解 易知 ∵ ……
各式相加得 ∴
点评:一般地,对于型如 类的通项公式,只要 能进行求和,则宜采用此方法求解。
例4. 若在数列 中, , ,求通项 。
解析:由 得 ,所以 , ,…, ,
将以上各式相加得: ,又 所以 =
例2: 已知数列{an}是公差为d的等差数列,数列{bn}是公比为q的(q∈R且q≠1)的等比数列,若函数f (x) = (x-1)2,且a1 = f (d-1),a3 = f (d+1),b1 = f (q+1),b3 = f (q-1),(1)求数列{ a n }和{ b n }的通项公式;
解:(1)∵a 1=f (d-1) = (d-2)2,a 3 = f (d+1)= d 2,∴a3-a1=d2-(d-2)2=2d=4,
∴d=2,∴an=a1+(n-1)d = 2(n-1);又b1= f (q+1)= q2,b3 =f (q-1)=(q-2)2,
∴ =q2,由q∈R,且q≠1,得q=-2,∴bn=b·qn-1=4·(-2)n-1
例1. 等差数列 是递减数列,且 =48, =12,则数列的通项公式是( )
(A) (B) (C) (D)
解析:设等差数列的公差位d,由已知 ,
解得 ,又 是递减数列, ∴ , ,∴ ,故选(D)。
例2. 已知等比数列 的首项 ,公比 ,设数列 的通项为 ,求数列 的通项公式。
解析:由题意, ,又 是等比数列,公比为
∴ ,故数列 是等比数列, ,∴
点评:当已知数列为等差或等比数列时,可直接利用等差或等比数列的通项公式,只需求得首项及公差公比。
例1:根据数列的前4项,写出它的一个通项公式:
(1)9,99,999,9999,…(2) (3) (4)
解:(1)变形为:101-1,102-1,103-1,104-1,…… ∴通项公式为:
(2) (3) (4) .点评:关键是找出各项与项数n的关系。
21.设函数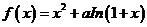 有两个极值点
有两个极值点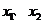 ,且
,且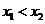
(I)求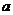 的取值范围,并讨论
的取值范围,并讨论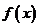 的单调性;
的单调性;
(II)证明: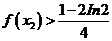
解: (I)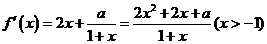
令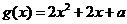 ,其对称轴为
,其对称轴为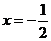 。由题意知
。由题意知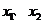 是方程
是方程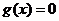 的两个均大于
的两个均大于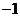 的不相等的实根,其充要条件为
的不相等的实根,其充要条件为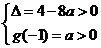 ,得
,得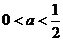
⑴当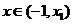 时,
时,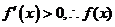 在
在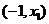 内为增函数;
内为增函数;
⑵当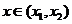 时,
时,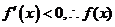 在
在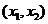 内为减函数;
内为减函数;
⑶当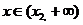 时,
时,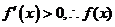 在
在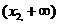 内为增函数;
内为增函数;
(II)由(I)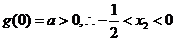 ,
,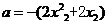
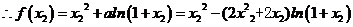
设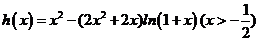 ,
,
则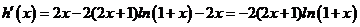
⑴当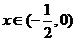 时,
时,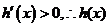 在
在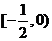 单调递增;
单调递增;
⑵当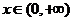 时,
时,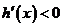 ,
,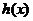 在
在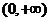 单调递减。
单调递减。
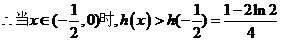
故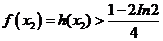 .
. 



20. 等比数列{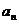 }的前n项和为
}的前n项和为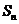 ,
已知对任意的
,
已知对任意的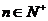 ,点
,点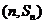 ,均在函数
,均在函数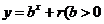 且
且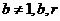 均为常数)的图像上.
均为常数)的图像上. 

(1)求r的值;
(11)当b=2时,记 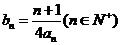 求数列
求数列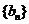 的前
的前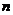 项和
项和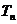
解:因为对任意的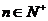 ,点
,点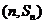 ,均在函数
,均在函数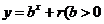 且
且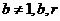 均为常数)的图像上.所以得
均为常数)的图像上.所以得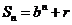 ,
,
当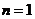 时,
时,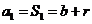 ,
, 

当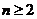 时,
时,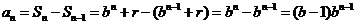 ,
,
又因为{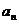 }为等比数列, 所以
}为等比数列, 所以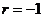 , 公比为
, 公比为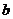 , 所以
, 所以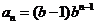
(2)当b=2时,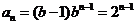 ,
, 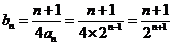
则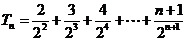
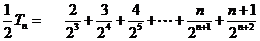


相减,得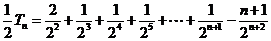
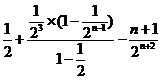
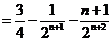
所以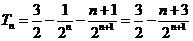
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com