6．(09年重庆文综15)隋唐时期，淮水以北新增的有利于农田灌溉的水利工程是　 　　　　　　　(　　　　 )

A．郑国渠　　 　　　　　　 B．芍陂　　 　　　　 C．通济渠　　　 　　 D．邗沟

答案　 C

5．(09上海文综30)中国古代艺术精彩纷呈，享誉世界，其中集彩塑、壁画和建筑艺术于一体的是 (　　　　 )

A．麦积山石窟　　　 　　　　　　　　　　　　　 B．敦煌莫高窟

C．大足石刻　　 　　　　　　　　　　　　　　　 　D．云冈石窟

答案　 B

4．(09年安徽文综14)西方学者查尔斯．默里在《文明的解析》一书中以下图表示公元600-1800年中国绘画的发展状况，约每200年间出现一个高峰。处于该图第一个高峰期的著名画家是 　　　　　　　(　　　　 )

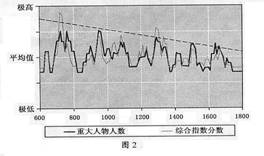
A．顾恺之　　 　　　　　　 B．吴道子　　 　　　 C．张择端　　 　　　 D．郑板桥

答案　 B

3．(09年辽宁宁夏文综26)北魏首创均田制，隋至唐初一直沿用。均田制下农业生产经营的主要形式是(　　　　 )

　A．众人集体生产　　　　 　　　　　　　　　　　 B．田庄规模生产

C．个体农户耕作　　　　 　　　　　　　　　　　 D．官府募民耕作

答案　 C

2．(09年全国Ⅱ卷文综13)隋唐时期商业经济较之前代有很大的发展，但仍有许多阻碍其进一步发展的因素，其中有　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　　　 )

A．废除五铢钱 　　　　　　　　　　 　　　　　　 B．市坊分区

C．实行两税法 　　　　　　　　　　 　　　　　　 D．草市兴起

答案　 B

1．(09年全国Ⅰ卷文综14)南朝秀美灵动，北朝刚健雄浑，南北文化共同孕育了唐朝文化的新气象。以下最能体现南方文化特征的是　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　　　 )

A．初唐书法　　 　　　　　 B．秦王破阵曲　　　 C．飞天壁画　　 　　 D．唐三彩

答案　 A

2009年高考题

3.形如 型

(1)若 (d为常数)，则数列{ }为“等和数列”，它是一个周期数列，周期为2，其通项分奇数项和偶数项来讨论;

(2)若f(n)为n的函数(非常数)时，可通过构造转化为 型，通过累加来求出通项;或用逐差法(两式相减)得 ，，分奇偶项来分求通项.

例1. 数列{ }满足 , ,求数列{a_n}的通项公式.

分析 1：构造 转化为 型

解法1：令

则 .

时,

各式相加:

当n为偶数时， .

此时

当n为奇数时，

此时 ,所以 .

故

解法2：

时， ，

两式相减得： .

构成以 ,为首项，以2为公差的等差数列;

构成以 ,为首项，以2为公差的等差数列

.

评注：结果要还原成n的表达式.

例2.(2005江西卷)已知数列{a_n}的前n项和S_n满足

S_n－S_n－2=3 求数列{a_n}的通项公式.

解：方法一：因为

　　 以下同例1，略

2.形如 型

(1)当f(n)为常数，即： (其中q是不为0的常数)，此时数列为等比数列， = .

(2)当f(n)为n的函数时,用累乘法.

　 由 得　　 时， ，

=f(n)f(n-1) .

例1.设 是首项为1的正项数列，且 ( =1，2， 3，…)，则它的通项公式是 =________.

解：已知等式可化为：

( ) (n+1) ,　 即

时，

= = .

评注：本题是关于 和 的二次齐次式，可以通过因式分解(一般情况时用求根公式)得到 与 的更为明显的关系式，从而求出 .

例2.已知 ,求数列{a_n}的通项公式.

解：因为 所以

故 又因为 ,即 ，

所以由上式可知 ,所以 ,故由累乘法得　

=

所以 -1.

评注：本题解题的关键是把原来的递推关系式 转化为

若令 ,则问题进一步转化为 形式，进而应用累乘法求出数列的通项公式.

除以上的转化方式外，还会出现多栋楼之间的联系，即不同数列之间的递推关系，对于该类问题，要整体考虑，根据所给数列递推公式的关系，灵活采用累加、累乘、化归等方法求解。

例题9：甲、乙两容器中分别盛有浓度为10%、20%的某种溶液500ml，同时从甲乙两个容器中取出100ml溶液，将近倒入对方的容器搅匀，这称为是一次调和，记a₁=10%,b₁=20%,经(n-1)次调和后甲、乙两个容器的溶液浓度为a­_n、b_n，

(1)试用a_n-1、b_n-1表示a­_n、b_n；

(2)求证数列 {a­_n-b_n}是等比数列，并求出a­_n、b_n的通项。

分析：该问题属于数列应用题，涉及到两个不同的数列a­_n和b_n，且这两者相互之间又有制约关系，所以不能单独地考虑某一个数列，而应该把两个数列相互联系起来。

解析：(1)由题意

；

(2)a­_n-b_n= = ( )(n≥2)， ∴{a­_n-b_n}是等比数列。

又a₁-b₁=-10%　　　 ∴a_n-b_­n­=-10%( ^n-1 ………(1)

又∵ = =…= a₁+b₁=30% ………(2)

联立(1)、(2)得 =-( ^n-1·5%+15%； =( ^n-1·5%+15%。

综而言之，等差、等比数列是两类最基本的数列，是数列部分的重点，自然也是高考考查的热点，而考查的目的在于测试灵活运用知识的能力，这个“灵活”往往集中在“转化”的水平上；以上介绍的仅是常见可求通项的递推数列的五种转化思路----“楼层式”的转化方式，同样采用相应的、风趣的教学形式，更易于学生接收新知识，从而激发学生的学习兴趣，让数学课堂生动活泼风趣起来。这正顺应了当前“新课程理念”的大趋势。

利用递推关系求数列通项的九种类型及解法

1.形如 型

(1)若f(n)为常数,即： ,此时数列为等差数列，则 = .

(2)若f(n)为n的函数时，用累加法.

方法如下： 由 得：

时， ，

，

所以各式相加得

即： .

为了书写方便，也可用横式来写：

　 时， ，

= .

例 1. (2003天津文) 已知数列{a_n}满足 ,

　　 证明

证明：由已知得：

　 = 　　 .

例2.已知数列 的首项为1，且 写出数列 的通项公式.　　　　　　　　　　　　　　　　 答案：

例3.已知数列 满足 ， ，求此数列的通项公式.　　　　　　　　　　　　　　　　　　　 答案： 　

评注：已知 , ，其中f(n)可以是关于n的一次函数、二次函数、指数函数、分式函数，求通项 .

①若f(n)是关于n的一次函数，累加后可转化为等差数列求和;

②若f(n)是关于n的二次函数，累加后可分组求和;

③若f(n)是关于n的指数函数，累加后可转化为等比数列求和;

④若f(n)是关于n的分式函数，累加后可裂项求和。

例4.已知数列 中, 且 ,求数列 的通项公式.

解:由已知 得 ,

化简有 ,由类型(1)有 ,

又 得 ,所以 ,又 , ,

则

此题也可以用数学归纳法来求解.