
19.(本小题满分12分)
袋中有大小、形状相同的红、黑球各一个,现一次有放回地随机摸取3次,每次摸取一个球
(I)试问:一共有多少种不同的结果?请列出所有可能的结果; 

(Ⅱ)若摸到红球时得2分,摸到黑球时得1分,求3次摸球所得总分为5的概率。
解:(I)一共有8种不同的结果,列举如下:
(红、红、红、)、(红、红、黑)、(红、黑、红)、(红、黑、黑)、(黑、红、红)、(黑、红、黑)、(黑、黑、红)、(黑、黑、黑)
(Ⅱ)记“3次摸球所得总分为5”为事件A
事件A包含的基本事件为:(红、红、黑)、(红、黑、红)、(黑、红、红)事件A包含的基本事件数为3
由(I)可知,基本事件总数为8,所以事件A的概率为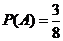
|
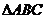 中,角
中,角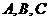 所对的边分别为
所对的边分别为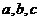 ,且满足
,且满足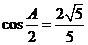 ,
,
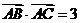 . (I)求
. (I)求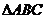 的面积; (II)若
的面积; (II)若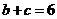 ,求
,求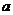 的值.
的值.
解析:(I)因为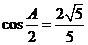 ,
,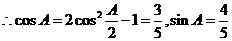 ,又由
,又由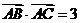 ,得
,得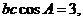
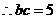 ,
,


(II)对于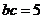 ,又
,又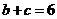 ,
,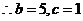 或
或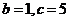 ,由余弦定理得
,由余弦定理得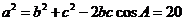 ,
,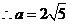


|
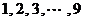 这
这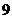 个自然数中,任取
个自然数中,任取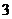 个数.
个数.
(I)求这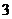 个数中恰有
个数中恰有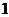 个是偶数的概率;
个是偶数的概率;
(II)设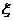 为这
为这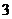 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为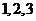 ,则有两组相邻的数
,则有两组相邻的数
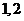 和
和 ,此时
,此时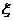 的值是
的值是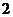 ).求随机变量
).求随机变量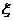 的分布列及其数学期望
的分布列及其数学期望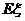 .
.
解析:(I)记“这3个数恰有一个是偶数”为事件A,则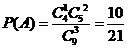 ;
; 

(II)随机变量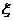 的取值为
的取值为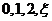 的分布列为
的分布列为
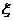 |
0 |
1 |
2 |
|
P |
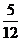 |
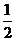 |
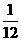 |
所以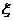 的数学期望为
的数学期望为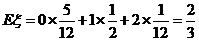


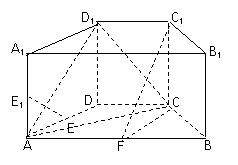
18.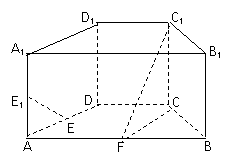 如图,在直四棱柱ABCD-A
如图,在直四棱柱ABCD-A B
B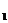 C
C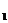 D
D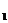 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA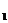 =2, E、E
=2, E、E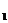 分别是棱AD、AA
分别是棱AD、AA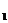 的中点.
的中点. 

(1) 设F是棱AB的中点,证明:直线EE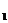 //平面FCC
//平面FCC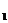 ;
;
(2) 证明:平面D1AC⊥平面BB1C1C.
证明:(1)在直四棱柱ABCD-A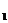 B
B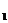 C
C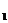 D
D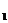 中,取A1B1的中点F1,
中,取A1B1的中点F1,
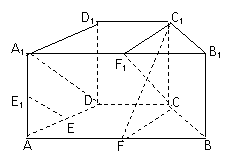 连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E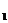 分别是棱AD、AA
分别是棱AD、AA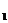 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为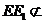 平面FCC
平面FCC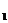 ,
,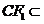 平面FCC
平面FCC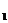 ,
,
所以直线EE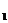 //平面FCC
//平面FCC .
.
 (2)连接AC,在直棱柱中,CC1⊥平面ABCD,AC
(2)连接AC,在直棱柱中,CC1⊥平面ABCD,AC 平面ABCD,
平面ABCD,
所以CC1⊥AC,因为底面ABCD为等腰梯形,AB=4, BC=2,
F是棱AB的中点,所以CF=CB=BF,△BCF为正三角形,
 ,△ACF为等腰三角形,且
,△ACF为等腰三角形,且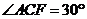
所以AC⊥BC, 又因为BC与CC1都在平面BB1C1C内且交于点C,
所以AC⊥平面BB1C1C,而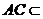 平面D1AC,
平面D1AC,
所以平面D1AC⊥平面BB1C1C.
15.等差数列{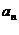 }前n项和为
}前n项和为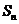 。已知
。已知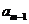 +
+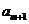 -
-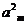 =0,
=0,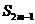 =38,则m=_______
=38,则m=_______
答案10
14. 已知函数y=sin(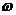 x+
x+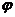 )(
)(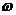 >0, -
>0, -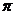
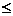
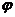 <
<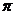 )的图像如图所示,则
)的图像如图所示,则 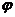 =________________
=________________
答案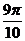
13.在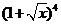 的展开式中,
的展开式中,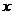 的系数为
(用数字作答).
的系数为
(用数字作答).
答案6
12.若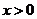 ,则
,则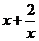 的最小值为
.
的最小值为
. 

答案2根号2
11.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项
运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为 .
答案12
10.设函数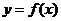 在
在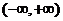 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数
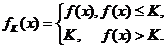
取函数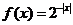 。当
。当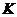 =
=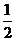 时,函数
时,函数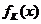 的单调递增区间为
的单调递增区间为
A .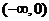 B.
B.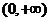 C .
C .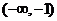 D .
D .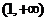
答案:C
9.若函数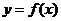 的导函数在区间
的导函数在区间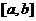 上是增函数,
上是增函数,
则函数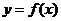
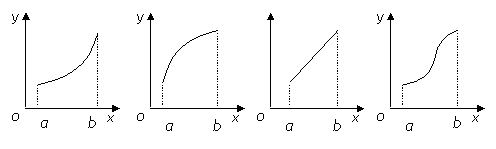 在区间
在区间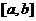 上的图象可能是
上的图象可能是
|
A . B. C. D.
答案:A
7.一个棱锥的三视图如图,则该棱锥的全面积(单位:c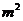 )为
)为
(A)48+12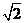 (B)48+24
(B)48+24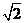 (C)36+12
(C)36+12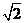 (D)36+24
(D)36+24
答案:A
8已知O,N,P在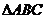 所在平面内,且
所在平面内,且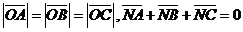 ,且
,且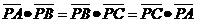 ,则点O,N,P依次是
,则点O,N,P依次是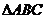 的
的
(A)重心 外心 垂心 (B)重心 外心 内心
(C)外心 重心 垂心 (D)外心 重心 内心
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com