
7.设f(x)=3ax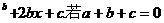 ,f(0)>0,f(1)>0,求证:
,f(0)>0,f(1)>0,求证:
(1)a>0且-2<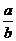 <-1;
<-1;
(2)方程f(x)=0在(0,1)内有两个实根.
6. 已知在二次函数的解析式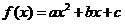 中,
中,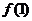 =-3,
=-3,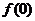 =-8,且它的两个零点间的距离等于2,求这个二次函数的解析式.
=-8,且它的两个零点间的距离等于2,求这个二次函数的解析式.
5.已知函数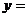
 对一切实数都有
对一切实数都有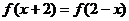 成立,且方程
成立,且方程 =0恰有6个不同的实根,则这6个根的和是
.
=0恰有6个不同的实根,则这6个根的和是
.
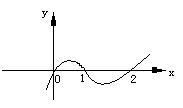
4.已知函数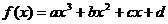 的图像如图所示,则b的取值范围是( )
的图像如图所示,则b的取值范围是( )
A.(-∞,0) B.(0,1) C.(1,2) D.(2,+∞)
3.若关于 的方程
的方程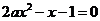 在(0,1)内恰有一解,则
在(0,1)内恰有一解,则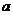 的取值范围为( )
的取值范围为( )
A. 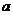 <-1 B.
<-1 B. 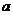 >1 C. -1<
>1 C. -1<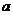 <1 D.0<
<1 D.0<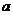 <1
<1
2.已知抛物线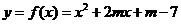 与
与 轴的两个交点在(1,0)两旁,则关于
轴的两个交点在(1,0)两旁,则关于 的方程
的方程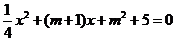 的根的情况是( )
的根的情况是( )
a.有两个正数根 B.有两个负数根
C.有一个正数根和一个负数根 D.无实数根
1. 方程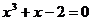 的实根的个数是( )
的实根的个数是( )
A. 0 B. 1 C. 2 D. 3.
[例1]已知函数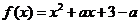 若
若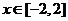 时,
时, ≥0恒成立,求
≥0恒成立,求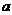 的取值范围.
的取值范围.
错解:(一)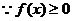 恒成立,∴△=
恒成立,∴△=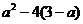 ≤0恒成立
≤0恒成立
解得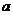 的取值范围为
的取值范围为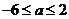
错解:(二)∵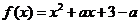 若
若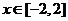 时,
时, ≥0恒成立
≥0恒成立
∴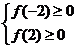 即
即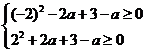
解得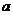 的取值范围为
的取值范围为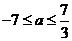
错因:对二次函数 =
=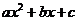 当
当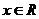 上
上 ≥0恒成立时,△≤0
≥0恒成立时,△≤0
片面理解为,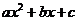 ≥0,
≥0,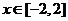 恒成立时,△≤0 ;或者理解为
恒成立时,△≤0 ;或者理解为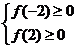
这都是由于函数性质掌握得不透彻而导致的错误.二次函数最值问题中“轴变区间定”要对对称轴进行分类讨论;“轴定区间变”要对区间进行讨论.
正解:设 的最小值为
的最小值为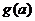
(1)当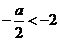 即
即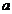 >4时,
>4时,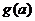 =
=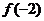 =7-3
=7-3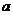 ≥0,得
≥0,得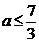 故此时
故此时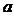 不存在;
不存在;
(2) 当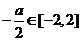 即-4≤
即-4≤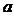 ≤4时,
≤4时,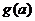 =3-
=3-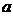 -
-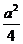 ≥0,得-6≤
≥0,得-6≤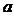 ≤2
≤2
又-4≤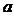 ≤4,故-4≤
≤4,故-4≤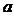 ≤2;
≤2;
(3)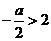 即
即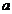 <-4时,
<-4时,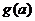 =
=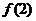 =7+
=7+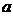 ≥0,得
≥0,得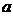 ≥-7,又
≥-7,又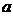 <-4
<-4
故-7≤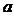 <-4
<-4
综上,得-7≤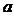 ≤2
≤2
[例2]已知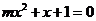 有且只有一根在区间(0,1)内,求
有且只有一根在区间(0,1)内,求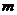 的取值范围.
的取值范围.
错解:设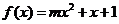 ∵
∵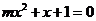 有且只有一根在区间(0,1)内
有且只有一根在区间(0,1)内
∴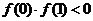 得
得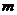 <-2
<-2
错因:对于一般 ,若
,若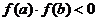 ,那么,函数
,那么,函数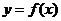 在区间(a,b)上至少有一个零点,但不一定唯一.对于二次函数
在区间(a,b)上至少有一个零点,但不一定唯一.对于二次函数 ,若
,若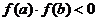 则在区间(a,b)上存在唯一的零点,一次函数有同样的结论成立.
则在区间(a,b)上存在唯一的零点,一次函数有同样的结论成立.
但方程 =0在区间(a,b)上有且只有一根时,不仅是
=0在区间(a,b)上有且只有一根时,不仅是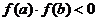 ,也有可能
,也有可能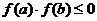 .如二次函数图像是下列这种情况时,就是这种情况.
.如二次函数图像是下列这种情况时,就是这种情况.
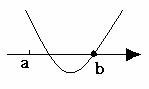 由图可知
由图可知 =0在区间(a,b)上有且只有一根,但是
=0在区间(a,b)上有且只有一根,但是
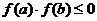
正解:设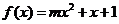 ,(1)当
,(1)当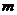 =0时方程的根为-1,不满足条件.
=0时方程的根为-1,不满足条件.
(2)当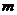 ≠0∵
≠0∵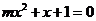 有且只有一根在区间(0,1)内
有且只有一根在区间(0,1)内
又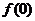 =1>0
=1>0
∴有两种可能情形①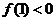 得
得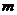 <-2
<-2
或者②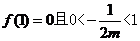 得
得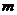 不存在
不存在
综上所得,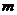 <-2
<-2
[例3]已知一次函数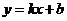 与二次函数
与二次函数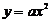 图像如图,其中
图像如图,其中
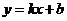 的交点与
的交点与 轴、
轴、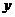 轴的交点分别为A(2,0),B(0,2);与二次函数
轴的交点分别为A(2,0),B(0,2);与二次函数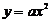 的交点为P、Q,P、Q两点的纵坐标之比为1︰4.(1)求这两个函数的解析式.(2)解方程:
的交点为P、Q,P、Q两点的纵坐标之比为1︰4.(1)求这两个函数的解析式.(2)解方程: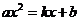
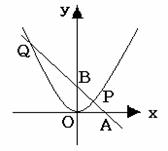 (1)错解:把 A(2,0),B(0,2)两点坐标分别代入一次函数
(1)错解:把 A(2,0),B(0,2)两点坐标分别代入一次函数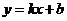 解得
解得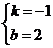
∴一次函数为 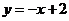
设P( 1,
1,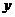 1),Q(,
1),Q(,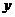 2),则
2),则
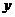 1︰
1︰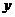 2=1︰4
2=1︰4
∴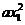 ︰
︰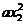 =1︰4 ∴
=1︰4 ∴ 1︰
1︰ 2=1︰2或
2=1︰2或 1︰
1︰ 2=(-1)︰2
2=(-1)︰2
当 1︰
1︰ 2=1︰2时,Q点坐标为(2
2=1︰2时,Q点坐标为(2 1,4
1,4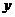 1),把P、Q两点坐标分别代入直线方程即得
1),把P、Q两点坐标分别代入直线方程即得 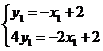 解得
解得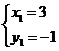
∴P(3,-1),Q(6,-4),抛物线方程为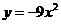
当 1︰
1︰ 2=(-1)︰2时, Q点坐标为(-2
2=(-1)︰2时, Q点坐标为(-2 1,4
1,4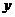 1)把P、Q两点坐标分别代入直线方程即得
1)把P、Q两点坐标分别代入直线方程即得 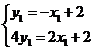 解得
解得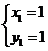
∴P(1, 1),Q(-2, 4),抛物线方程为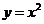
错因:在得到 1︰
1︰ 2值之后,要注意题意判断点的位置关系,多余的解要舍去,题中Q在第二象限,所以
2值之后,要注意题意判断点的位置关系,多余的解要舍去,题中Q在第二象限,所以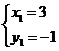 不合条件.
不合条件.
正解:(1)抛物线方程为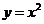
(2)方法一:由(1)得方程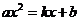 即为
即为 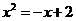
解得 1=-2,
1=-2, 2=1.
2=1.
方法二:方程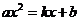 的根即为二次函数
的根即为二次函数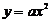 与一次函数
与一次函数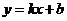 的交点的横坐标.由(1)知它们交点的坐标分别为P(1, 1),Q(-2, 4),
的交点的横坐标.由(1)知它们交点的坐标分别为P(1, 1),Q(-2, 4),
∴方程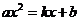 的解为
的解为 1=-2,
1=-2, 2=1.
2=1.
[例4]是否存在这样的实数k,使得关于x的方程
 2+(2k-3)
2+(2k-3) -(3k-1)=0有两个实数根,且两根都在0与2之间?如果有,试确定k的取值范围;如果没有,试说明理由.
-(3k-1)=0有两个实数根,且两根都在0与2之间?如果有,试确定k的取值范围;如果没有,试说明理由.
错解:令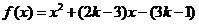 那么由条件得到
那么由条件得到
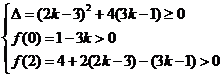 即此不等式无解
即此不等式无解
即不存在满足条件的k值.
错因:方程两根都在0与2之间,根据图像,可知除满足上述条件外,还要考虑二次函数的对称轴在区间(0,2)内.
正解:令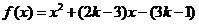 那么由条件得到
那么由条件得到
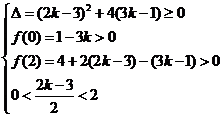 即
即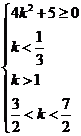 即此不等式无解
即此不等式无解
即不存在满足条件的k值.
[例5]已知二次函数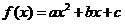 对于
对于 1、
1、 2
2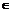 R,且
R,且 1<
1< 2时
2时
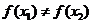 ,求证:方程
,求证:方程 =
=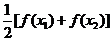 有不等实根,且必有一根属于区间(
有不等实根,且必有一根属于区间( 1,
1, 2).
2).
解:设F( )=
)= -
-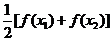 ,
,
则方程  =
=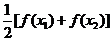 ①
①
与方程 F( )=0 ② 等价
)=0 ② 等价
∵F( 1)=
1)=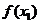 -
-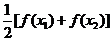 =
=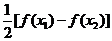
F( 2)=
2)=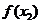 -
-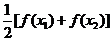 =
=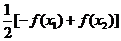
∴ F( 1)·F(
1)·F( 2)=-
2)=-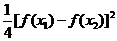 ,又
,又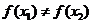
∴F( 1)·F(
1)·F( 2)<0
2)<0
故方程②必有一根在区间( 1,
1, 2)内.由于抛物线y=F(
2)内.由于抛物线y=F( )在
)在 轴上、下方均有分布,所以此抛物线与
轴上、下方均有分布,所以此抛物线与 轴相交于两个不同的交点,即方程②有两个不等的实根,从而方程①有两个不等的实根,且必有一根属于区间(
轴相交于两个不同的交点,即方程②有两个不等的实根,从而方程①有两个不等的实根,且必有一根属于区间( 1,
1, 2).
2).
点评:本题由于方程是 =
=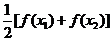 ,其中因为有
,其中因为有 表达式,所以解题中有的学生不理解函数图像与方程的根的联系,误认为证明
表达式,所以解题中有的学生不理解函数图像与方程的根的联系,误认为证明 的图像与
的图像与 轴相交于两个不同的点,从而证题中着眼于证
轴相交于两个不同的点,从而证题中着眼于证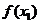
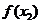 <0,使本题没法解决. 本题中将问题转化为F(
<0,使本题没法解决. 本题中将问题转化为F( )=
)= -
-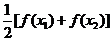 的图像与
的图像与 轴相交于两个不同的两点是解题的关健所在.
轴相交于两个不同的两点是解题的关健所在.
[例6]试确定方程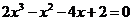 最小根所在的区间,并使区间两个端点是两个连续的整数.
最小根所在的区间,并使区间两个端点是两个连续的整数.
分析:只要构造函数 =
=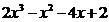 ,计算
,计算 的自变量
的自变量 取整数值时的函数值,根据其符号,确定方程根的个数及根的分布.
取整数值时的函数值,根据其符号,确定方程根的个数及根的分布.
解:令 =
=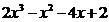
∵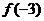 =-54-9+12+2=-49<0
=-54-9+12+2=-49<0
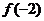 =-16-4+8+2=-10<0
=-16-4+8+2=-10<0
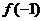 =-2-1+4+2=3>0
=-2-1+4+2=3>0
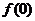 =0-0-0+2=2>0
=0-0-0+2=2>0
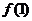 =2-1-4+2=-1<0
=2-1-4+2=-1<0
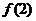 =16-4-8+2=6>0
=16-4-8+2=6>0
根据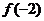 ·
·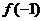 <0,
<0,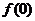 ·
·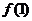 <0,
<0,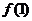 ·
·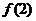 <0
<0
可知 的零点分别在区间(-2,-1),(0,1),(1,2)内.
的零点分别在区间(-2,-1),(0,1),(1,2)内.
因为方程是一个一元三次方程,所以它最多有三个根,所以原方程的最小根在区间(-2,-1)内.
点评:计算一元高次函数值可借助于计算器来完成,在实数范围内一元n次方程最多有n个实根,当然本题也可以用因式分解方法来解.
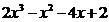
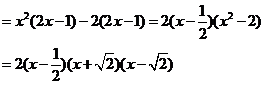
所以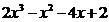 =0有三个根:
=0有三个根: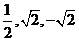
[例7]设二次函数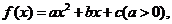 方程
方程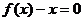 的两个根
的两个根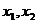 ,满足0
,满足0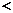
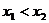
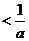 .
.
(1)当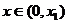 时,证明
时,证明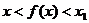 ;
;
(2)设函数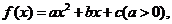 的图像关于直线
的图像关于直线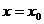 对称,证明:
对称,证明:
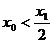 .
.
分析:(1)用作差比较法证明不等式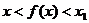 ;
;
(2)函数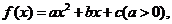 图像关于直线
图像关于直线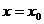 对称,实际直线
对称,实际直线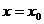 就是二次函数的对称轴,即
就是二次函数的对称轴,即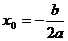 ,然后用已知条件证明不等式即可.
,然后用已知条件证明不等式即可.
证明:(1)依题意,设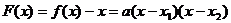
当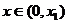 时,由于
时,由于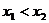 ,∴
,∴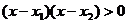 ,又
,又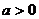
∴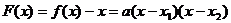 >0即
>0即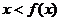
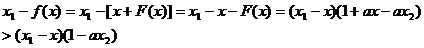
∵0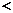
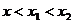
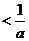 .∴
.∴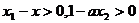
∴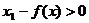
综合得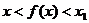
(2)依题意知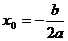 ,又
,又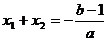
∴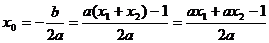
∵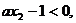 ∴
∴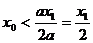
点评:解决本题的关健有三:一是用作差比较法证明不等式;二是正确选择二次函数的表达式,即本题选用两根式表示;三要知道二次函数的图像关于直线对称,此直线为二次函数的对称轴,即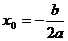
[例8] 已知函数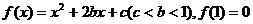 ,且方程
,且方程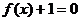 有实根.
有实根.
(1)求证:-3<c≤-1,b≥0.
(2)若m是方程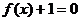 的一个实根,判断
的一个实根,判断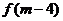 的正负并加以证明
的正负并加以证明
分析:(1)题中条件涉及不等关系的有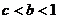 和方程
和方程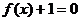 有实根.
有实根.
及一个等式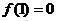 ,通过适当代换及不等式性质可解得;(2)本小题只要判断
,通过适当代换及不等式性质可解得;(2)本小题只要判断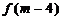 的符号,因而只要研究出
的符号,因而只要研究出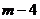 值的范围即可定出
值的范围即可定出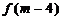 符号.
符号.
(1)证明:由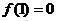 ,得1+2b+c=0,解得
,得1+2b+c=0,解得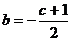 ,又
,又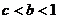 ,
,
1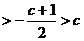
解得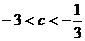 ,
,
又由于方程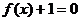 有实根,即
有实根,即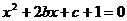 有实根,
有实根,
故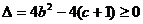 即
即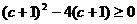 解得
解得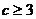 或
或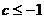
∴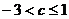 ,由
,由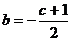 ,得
,得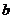 ≥0.
≥0.
(2)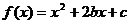 =
=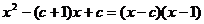
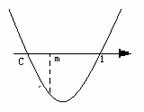 ∵
∵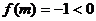 ,∴c<m<1(如图)
,∴c<m<1(如图)
∴c-4<m-4<-3<c.
∴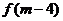 的符号为正.
的符号为正.
点评:二次函数值的符号,可以求出其值判断,也可以灵活运用二次函数的图像及性质解题.
4.用二分法求二次方程的近似解一般步骤是
(1)取一个区间(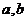 )使
)使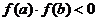
(2)取区间的中点,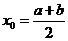
(3)计算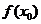 ,①若
,①若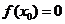 ,则
,则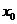 就是
就是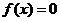 的解,计算终止;②若
的解,计算终止;②若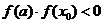 ,则解位于区间(
,则解位于区间(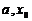 )中,令
)中,令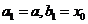 ;若
;若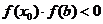 则解位于区间(
则解位于区间(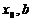 )令
)令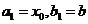
(4)取区间是(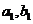 )的中点,
)的中点,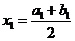 重服第二步、第三骤直到第n步,方程的解总位于区间(
重服第二步、第三骤直到第n步,方程的解总位于区间(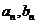 )内
)内
(5)当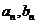 精确到规定的精确度的近似值相等时,那么这个值就是所求的近似解.
精确到规定的精确度的近似值相等时,那么这个值就是所求的近似解.
3. 二次方程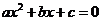 的根在某一区间时,满足的条件应据具体情形而定.如二次方程
的根在某一区间时,满足的条件应据具体情形而定.如二次方程 =
=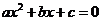 的根都在区间
的根都在区间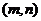 时
时
应满足: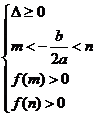
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com