
7.已知函数f(x)满足f(logax)=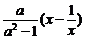 (其中a>0,a≠1,x>0),求f(x)的表达式.
(其中a>0,a≠1,x>0),求f(x)的表达式.
6.已知函数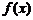 满足:
满足: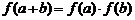 ,
,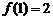 ,则
,则
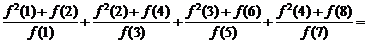 .
.
5. 若函数f(x)=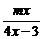 (x≠
(x≠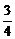 )在定义域内恒有f[f(x)]=x,则m等于( )
)在定义域内恒有f[f(x)]=x,则m等于( )
A.3 B.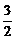 C.-
C.-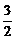 D.-3
D.-3
4.函数f(x)=的最小值为
A.190 B.171 C.90 D.45
3.方程f(x,y)=0的曲线如图所示,那么方程f(2-x,y)=0的曲线是 ( )
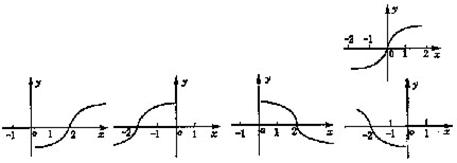

2.对函数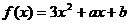 作代换x=g(t),则总不改变f(x)值域的代换是( ) A.
作代换x=g(t),则总不改变f(x)值域的代换是( ) A.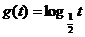 B.
B.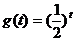
C.g(t)=(t-1)2 D.g(t)=cost
1. 已知函数f(x),x∈F,那么集合{(x,y)|y=f(x),x∈F}∩{(x,y)|x=1}中所含元素的个数是( )

A.0 B.1 C.0或1 D.1或2
[例1]设M={a,b,c},N={-2,0,2},求(1)从M到N的映射种数;

(2)从M到N的映射满足 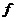 (a)>
(a)>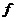 (b)≥f(c),试确定这样的映射
(b)≥f(c),试确定这样的映射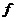 的种数.
的种数.

错解:(1)由于M={a,b,c},N={-2,0,2},结合映射的概念,有

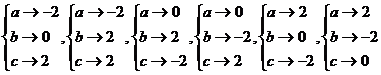 ,共6个映射
,共6个映射

(2)由(1)得满足条件的映射仅有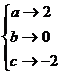 一种情况
一种情况

错因:没有找全满足条件的映射个数,关健是对概念认识不清

正解:(1)由于M={a,b,c},N={-2,0,2},结合映射的概念,有

一共有27个映射

(2)符合条件的映射共有4个


[例2]已知函数 的定义域为[0,1],求函数
的定义域为[0,1],求函数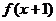 的定义域
的定义域

错解:由于函数 的定义域为[0,1],即
的定义域为[0,1],即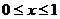 ,
,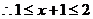


∴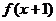 的定义域是[1,2]
的定义域是[1,2]

错因:对函数定义域理解不透,不明白 与
与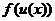 定义域之间的区别与联系,其实在这里只要明白:
定义域之间的区别与联系,其实在这里只要明白: 中
中 取值的范围与
取值的范围与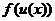 中式子
中式子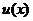 的取值范围一致就好了.
的取值范围一致就好了.

正解:由于函数 的定义域为[0,1],即
的定义域为[0,1],即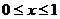 ∴
∴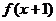 满足
满足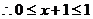


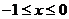 ,∴
,∴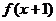 的定义域是[-1,0]
的定义域是[-1,0]

[例3]已知: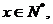
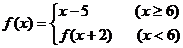 ,求
,求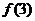 .
.

错解:∵ 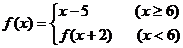 ,∴
,∴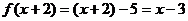


故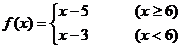 ,∴
,∴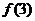 =3-3=0.
=3-3=0.

错因:没有理解分段函数的意义,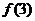 的自变量是3,应代入
的自变量是3,应代入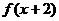 中去,而不是代入
中去,而不是代入 -5中,只有将自变量化为不小于6的数才能代入解析式求解.
-5中,只有将自变量化为不小于6的数才能代入解析式求解.

正解:∵ 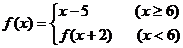 ,
,

∴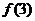 =
=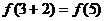 =
=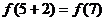 =7-5=2
=7-5=2 

[例4]已知 的反函数是
的反函数是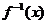 ,如果
,如果 与
与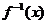 的图像有交点,那么交点必在直线
的图像有交点,那么交点必在直线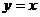 上,判断此命题是否正确?
上,判断此命题是否正确? 

错解:正确

错因:对互为反函数的图像关于直线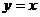 对称这一性质理解不深,比如函数
对称这一性质理解不深,比如函数

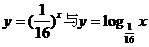 的图像的交点中,点
的图像的交点中,点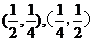 不在直线
不在直线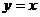 上,由此可以说明“两互为反函数图像的交点必在直线
上,由此可以说明“两互为反函数图像的交点必在直线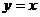 上”是不正确的.
上”是不正确的.

[例5]求函数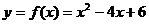 ,
,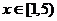 的值域.
的值域.

错解: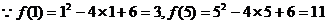


又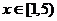 ,
,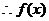 的值域是
的值域是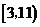


错因:对函数定义中,输入定义域中每一个x值都有唯一的y值与之对应,错误地理解为x的两端点时函数值就是y的取值范围了.

正解:配方,得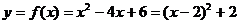


∵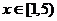 ,对称轴是
,对称轴是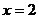 ∴当
∴当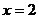 时,函数取最小值为
时,函数取最小值为 2,
2,




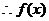 的值域是
的值域是


[例6]已知 ,求函数
,求函数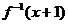 的解析式.
的解析式.

错解:由已知得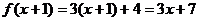


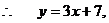 即
即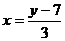 ,∴
,∴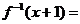
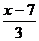


错因:将函数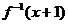 错误地认为是
错误地认为是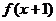 的反函数,是由于对函数表达式理解不透彻所致,实际上
的反函数,是由于对函数表达式理解不透彻所致,实际上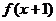 与
与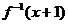 并不是互为反函数,一般地应该由
并不是互为反函数,一般地应该由 先求
先求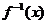 ,再去得到
,再去得到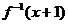 .
.

正解:因为 的反函数为
的反函数为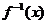 =
= ,
,

所以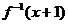 =
=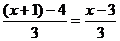 =
=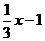


[例7]根据条件求下列各函数的解析式:

(1)已知 是二次函数,若
是二次函数,若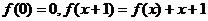 ,求
,求 .
.

(2)已知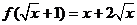 ,求
,求


(3)若 满足
满足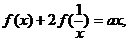 求
求


解:(1)本题知道函数的类型,可采用待定系数法求解

设 =
=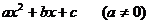 由于
由于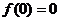 得
得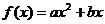 ,
,

又由 ,∴
,∴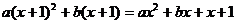


即 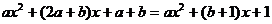


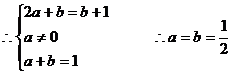 因此:
因此: =
=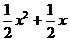


(2)本题属于复合函数解析式问题,可采用换元法求解

 设
设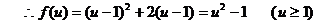


∴ =
=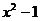 (
(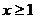 )
)

(3)由于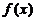 为抽象函数,可以用消参法求解
为抽象函数,可以用消参法求解

用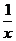 代
代 可得:
可得: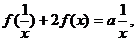


与 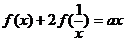


联列可消去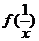 得:
得: =
=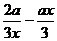 .
.

点评:求函数解析式(1)若已知函数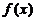 的类型,常采用待定系数法;(2)若已知
的类型,常采用待定系数法;(2)若已知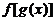 表达式,常采用换元法或采用凑合法;(3)若为抽象函数,常采用代换后消参法.
表达式,常采用换元法或采用凑合法;(3)若为抽象函数,常采用代换后消参法.

[例8] 已知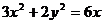 ,试求
,试求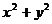 的最大值.
的最大值.

分析:要求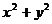 的最大值,由已知条件很快将
的最大值,由已知条件很快将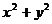 变为一元二次函数
变为一元二次函数 然后求极值点的
然后求极值点的 值,联系到
值,联系到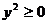 ,这一条件,既快又准地求出最大值.
,这一条件,既快又准地求出最大值.

解 由  得
得




又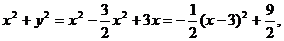


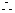 当
当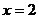 时,
时,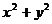 有最大值,最大值为
有最大值,最大值为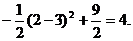


点评:上述解法观察到了隐蔽条件,体现了思维的深刻性.大部分学生的作法如下:

由 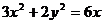 得
得 


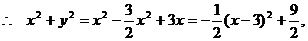


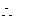 当
当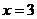 时,
时,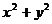 取最大值,最大值为
取最大值,最大值为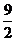


这种解法由于忽略了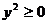 这一条件,致使计算结果出现错误.因此,要注意审题,不仅能从表面形式上发现特点,而且还能从已知条件中发现其隐蔽条件,既要注意主要的已知条件,又要注意次要条件,甚至有些问题的观察要从相应的图像着手,这样才能正确地解题..
这一条件,致使计算结果出现错误.因此,要注意审题,不仅能从表面形式上发现特点,而且还能从已知条件中发现其隐蔽条件,既要注意主要的已知条件,又要注意次要条件,甚至有些问题的观察要从相应的图像着手,这样才能正确地解题..

[例9]设 是R上的函数,且满足
是R上的函数,且满足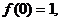 并且对任意的实数
并且对任意的实数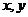 都有
都有

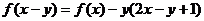 ,求
,求 的表达式.
的表达式.

解法一:由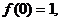
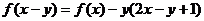 ,设
,设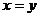 ,
,

得 ,所以
,所以 =
=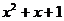


解法二:令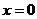 ,得
,得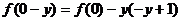


即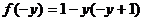


又将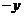 用
用 代换到上式中得
代换到上式中得 =
=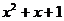


点评:所给函数中含有两个变量时,可对这两个变量交替用特殊值代入,或使这两个变量相等代入,再用已知条件,可求出未知的函数.具体取什么特殊值,根据题目特征而定.

3.对反函数概念的认识

(1)函数y= 只有满足是从定义域到值域上一一映射,才有反函数;
只有满足是从定义域到值域上一一映射,才有反函数;

(2)反函数的定义域和值域分别是原函数的值域和定义域,因此反函数的定义域一般不能由其解析式来求,而应该通过原函数的值域而得.

(3)互为反函数的函数有相同的单调性,它们的图像关于y=x对称.

2.对函数概念的认识

(1)对函数符号  的理解知道 y=
的理解知道 y= 与
与  的含义是一样的,它们都表示
的含义是一样的,它们都表示 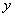 是
是  的函数,其中
的函数,其中 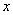 是自变量,
是自变量, 是函数值,连接的纽带是法则
是函数值,连接的纽带是法则 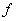 .
.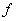 是单值对应.
是单值对应.

(2)注意定义中的集合 A,B都是非空的数集,而不能是其他集合;

(3)函数的三种表示法:解析法,列表法,和图像法.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com